Funkcja kwadratowa \(f\) jest określona dla wszystkich liczb rzeczywistych \(x\) wzorem \(f(x)=ax^2+bx+c\). Największa wartość funkcji \(f\) jest równa \(6\) oraz \(f(-6)=f(0)=\frac{3}{2}\). Oblicz wartość współczynnika \(a\).
Na podstawie danych z treści zadania możemy naszkicować parabolę i spróbujmy zrobić to dość dokładnie, czyli tak aby przecięła nam oś igreków w punkcie \(y=\frac{3}{2}\) (bo \(f(0)=\frac{3}{2}\)) no i tak, żeby miała najwyższą wartość równą \(6\). I tu też ważna uwaga – skąd mamy wiedzieć, czy ramiona tej paraboli są skierowane do dołu czy do góry? Skoro funkcja kwadratowa przyjmuje jakąś największą wartość, no to jej wierzchołek musi być na samej górze paraboli, więc ramiona będą skierowane do dołu.
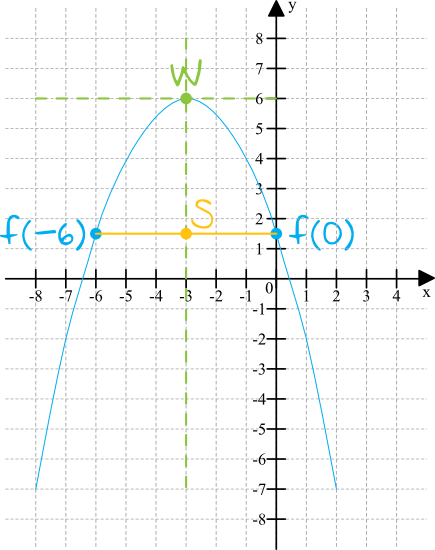
Dodatkowo zaznaczyłem na rysunku punkt \(S\). Jest to środek odcinka \(AB\). Przyda nam się on do zrozumienia tego jak obliczyć brakującą współrzędną wierzchołka.
Wiemy, że nasz wierzchołek ma współrzędne \(W=(p;6)\). Brakuje nam pierwszej współrzędnej, ale wiemy że będzie ona jednakowa jak współrzędna iksowa punktu \(S\), bo wierzchołek leży dokładnie nad punktem \(S\). Zatem współrzędna iksowa wierzchołka może zostać wyliczona ze wzoru na środek odcinka \(AB\):
$$p=\frac{x_{A}+x_{B}}{2} \\
p=\frac{-6+0}{2} \\
p=-3$$
To oznacza, że znamy już pełne współrzędne wierzchołka paraboli \(P=(-3;6)\).
Znając współrzędne wierzchołka możemy skorzystać z postaci kanonicznej funkcji kwadratowej:
$$f(x)=a(x-p)^2+q \\
f(x)=a(x-(-3))^2+6 \\
f(x)=a(x+3)^2+6$$
Do powyższego wzoru funkcji wystarczy już tylko podstawić współrzędne jednego ze znanych nam punktów (musi to być inny punkt niż wierzchołek). Podstawmy więc współrzędne punktu przecięcia się paraboli z osią igreków, czyli \((0;\frac{3}{2})\) i tym samym wyznaczymy poszukiwaną wartość współczynnika \(a\):
$$f(x)=a(x+3)^2+6 \\
\frac{3}{2}=a(0+3)^2+6 \\
\frac{3}{2}=9a+6 \\
\frac{3}{2}=9a+\frac{12}{2} \\
9a=-\frac{9}{2} \\
a=-\frac{1}{2}$$
\(a=-\frac{1}{2}\)


O jejku jak łatwo można to zrobić a ja kombinowałam z wyznaczania c z wzoru na q i podstawiania do równania (i tak nie wyszło)…
ja mam pytanie, skoro parabola jest skierowana ku górze, to dlaczego współczynnik a wychodzi na minusie, pozdrawiam, świetna strona :)
Ale ta parabola nie jest skierowana ku górze! ;) Ona ma RAMIONA skierowane do dołu, stąd też współczynnik a jest ujemny.
Rozumiem na czym polega Twój błąd – analizujesz ten „garb” paraboli, a analizuje się ramiona ;)
– jeżeli ramiona są skierowane do góry, to współczynnik a jest dodatni
– jeżeli ramiona są skierowane do dołu, to współczynnik a jest ujemny
A jak obliczyć w tym zadaniu pozostałe współczynniki b,c?
Jak już wiemy, że a=1/2 to mamy pełny wzór funkcji, czyli f(x)=1/2*(x+3)^2+6. Wystarczy teraz wykonać potęgowanie i uprościć cały zapis, otrzymamy wtedy postać ogólną, czyli poznamy współczynniki b oraz c :) Pamiętaj tylko o wzorach skróconego mnożenia przy potęgowaniu!
Uwielbiam tę stronę, wszystko jest wytłumaczone bardzo logicznie i przystępnie! Jednak mam pewne pytanie. Dlaczego przy podstawianiu współrzędnych do wzoru musi to być inny punkt niż wierzchołek? (krok 4) Z góry dziękuję za odpowiedź :)
Bardzo dobre pytanie! ;) Jeśli podstawimy współrzędne wierzchołka, to w nawiasie (x-3) wyjdzie nam 0, przez co będziemy mieć tak naprawdę 0a. No i to jest sytuacja niepożądana, bo my chcemy ten współczynnik a jakoś wyliczyć zamiast pozbywać :D
Mam pytanie, apropo pierwszego kroku. Jakby to wyglądało posługując się samymi wzorami?
Pozdrawiam :)
Powiem szczerze, że nie bardzo wiem co masz na myśli ;) W pierwszym kroku dokonujemy analizy sytuacji na podstawie danych z treści zadania i generalnie nie opieramy się tutaj na jakimś wzorze jako takim, tylko szkicujemy sytuację na podstawie znanych informacji :)
Można też układami równań f(0)=3/2; f(0) = c; c=3/2
x=(-6) dla y=3/2
x=p dla y=q czyli x=(-3) dla y=3/2
podstawić do wzoru: f(x)=y=ax^2+bx+c
{3/2=36a-6b+3/2
{6=9a-3b+3/2
z pierwszego:
6b=36a
b=6a
z drugiego:
6=9a-3b+3/2 // za b podstawiamy 6a
6=9a-18a+3/2 //*2
12=18a-36a+3 //-3
9=18a-36a //:9
1=2a-4a
1=(-2)a
-1/2=a
b=6a
b=(-1/2)*6
b=(-6)/2
b=(-3)
mam pytanie, dlaczego możemy traktować -6 i 0 jako współrzędne do paraboli skoro ich y nie jest równy 0? myślałem, że tylko jeśli y=0 to wtedy mamy nasze x1 i x2
Domyślam się, że w tym pytaniu chodzi o to, że zazwyczaj współrzędną p wierzchołka paraboli obliczamy jako średnią arytmetyczną miejsc zerowych (czyli tam gdzie y=0), no a tu mamy faktycznie przykład w którym tą współrzędną p obliczamy z nieco innych miejsc :) Ten sposób jest dobry, bo wyznaczanie współrzędnej p tak naprawdę opiera się na tym, żeby brać do obliczeń dwa argumenty, dla których funkcja przyjmuje jednakową wartość (nie muszą to być miejsca zerowe). To nawet na wykresie ładnie widać, że od argumentu x=-6 do wierzchołka dzieli nas tyle samo co od wierzchołka do argumentu x=0 ;)