Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Kojarząc jak wygląda wykres funkcji kwadratowej \(f(x)=x^2\), powinniśmy samodzielnie przekształcić jej wykres do postaci \(f(x)=-x^2+4\) (minus przed \(x^2\) sprawia, że funkcję opisaną wzorem \(x^2\) musimy narysować do góry nogami, a \(+4\) na końcu wzoru oznacza, że dodatkowo całość trzeba podnieść o \(4\) jednostki do góry). Całość będzie wyglądać następująco:
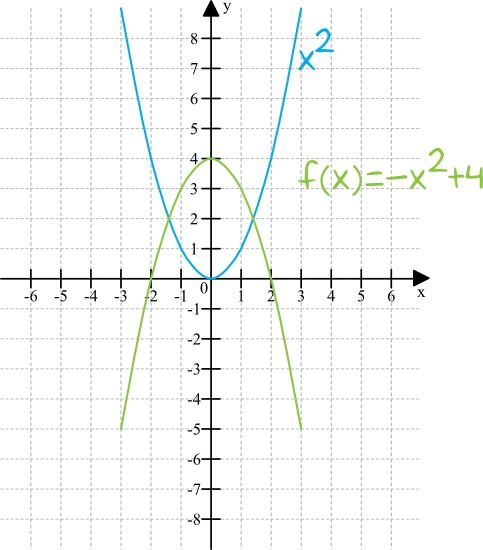
Krok 2. Odczytanie zbioru wartości funkcji.
Spoglądamy na naszą zieloną funkcję i na oś \(OY\), bo to z niej odczytujemy wartości przyjmowane przez funkcję. Widzimy wyraźnie, że funkcja ta przyjmuje wartości od minus nieskończoności do \(4\), zatem zbiorem wartości jest przedział \((-\infty,4\rangle\).