Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować szkice dwóch brył, które są przedmiotem naszego zadania, nanosząc od razu dane z treści zadania:
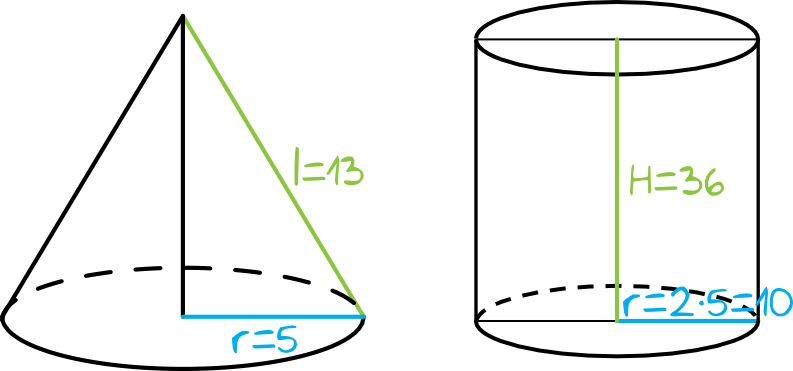
Krok 2. Obliczenie wysokości stożka (foremki).
Generalnie istota zadania opiera się na tym by obliczyć objętość dwóch naszkicowanych przed chwilą brył. Obliczenie wartości walca jest proste, bo mamy wszystkie potrzebne dane. Nieco gorzej jest ze stożkiem, bo tutaj brakuje nam wysokości tej bryły. Musimy zatem na samym początku obliczyć długość tej wysokości, a pomoże nam w tym Twierdzenie Pitagorasa:
$$5^2+H^2=13^2 \\
25+H^2=169 \\
H^2=144 \\
H=12$$
Krok 3. Obliczenie objętości stożka (foremki).
Obliczenia objętości brył zaczniemy od obliczenia objętości stożka, a w tym pomoże nam wzór na objętość tej bryły, który ma następującą postać:
$$V=\frac{1}{3}P_{p}\cdot H$$
Z racji tego iż w podstawie mamy koło, to pod \(P_{p}\) możemy podstawić wzór na pole koła, czyli \(πr^2\). Promień tego koła jest znany (\(r=5\)), wysokość obliczyliśmy w poprzednim kroku (\(H=12\)), zatem teraz bez przeszkód obliczymy objętość stożka:
$$V=\frac{1}{3}πr^2\cdot H \\
V=\frac{1}{3}π\cdot5^2\cdot12 \\
V=\frac{1}{3}π\cdot5^2\cdot12 \\
V=4π\cdot25 \\
V=100π$$
Krok 4. Obliczenie objętości walca (wiaderka).
Wiaderko ma promień podstawy równy dwukrotności promienia podstawy foremki, czyli:
$$r=2\cdot5cm=10cm$$
Wiemy już, że w podstawie znajduje się koło o promieniu \(r=10cm\), dodatkowo z treści zadania wiemy że wysokość walca jest równa \(H=36cm\), czyli objętość walca będzie równa:
$$V=P_{p}\cdot H \\
V=πr^2\cdot H \\
V=π\cdot10^2\cdot36 \\
V=100π\cdot36 \\
V=3600π$$
Krok 5. Obliczenie jaka część wiaderka została wypełniona.
Dziecko do wiaderka wrzuciło \(6\) foremek piasku, z czego każda ma objętość \(V=100π\). Zatem wrzucona objętość wynosi \(6\cdot100π=600π\). Wiaderko ma objętość \(3600π\), zatem piasek z sześciu foremek stanowi:
$$\frac{600π}{3600π}=\frac{1}{6}$$