Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Jeżeli trójkąt \(ADB\) jest równoramienny (a tak wynika z założeń), to znaczy że kąty przy boku \(AB\) mają jednakową miarę. Skoro tak, to kąt \(DBC\) będzie miał także tą samą miarę. Dlaczego? Skoro prosta \(BD\) jest dwusieczną kąta \(ABC\), to \(|\sphericalangle ABD|=|\sphericalangle DBC|\). Całość na rysunku wyglądać będzie następująco:
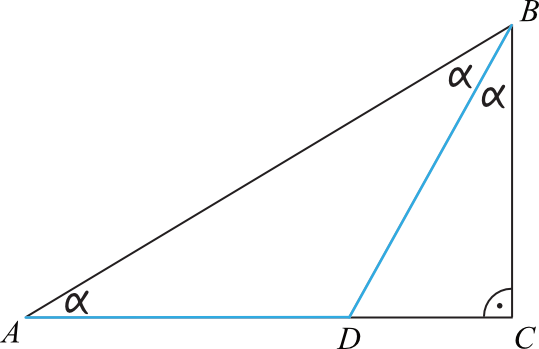
Krok 2. Obliczenie miary kąta \(α\).
Spójrzmy na trójkąt \(ABC\). W trójkącie suma kątów jest równa \(180°\). Jeden z kątów tego trójkąta już znamy i jest to kąt \(90°\). To oznacza, że na dwa pozostałe kąty zostaje nam \(180°-90°=90°\). Jeżeli przyjrzymy się rysunkowi to zauważymy, że pozostałe kąty mają łączną miarę \(α+2α=3α\). Zatem:
$$3α=90° \\
α=30°$$
Krok 3. Zakończenie dowodzenia.
Dowodzenie możemy zakończyć na różne sposoby - przykładowo możemy zapisać, że trójkąt \(BCD\) jest trójkątem o kątach \(30°,60°,90°\), zatem z własności tego trójkąta wynika, że jeżeli przyprostokątną DC oznaczymy jako \(a\), to przeciwprostokątna \(BD\) jest równa \(2a\), czyli zajdzie równość \(|CD|=\frac{1}{2}\cdot |BD|\).
Jeszcze lepiej zakończenie dowodzenia będzie wyglądać jak skorzystamy po prostu z funkcji trygonometrycznych, a konkretnie z sinusa:
$$sin30°=\frac{|CD|}{|DB|} \\
\frac{1}{2}=\frac{|CD|}{|DB|} \quad\bigg/\cdot |DB| \\
|CD|=\frac{1}{2}\cdot |BD|$$