Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Jeżeli trzy z czterech kątów mają miarę \(225°\), to czwarty kąt musi mieć miarę:
$$360°-225°=135°$$
Całość więc wygląda w następujący sposób.
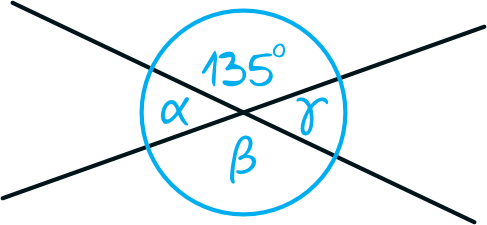
Krok 2. Wyznaczenie miary kątów ostrych.
Spójrzmy na kąt \(α\). Jest on kątem przyległym do kąta \(135°\), zatem jego miara musi wynosić:
$$180°-135°=45°$$
Dokładnie ta sama sytuacja jest z kątem \(γ\), jego miara to także \(45°\).
Krok 3. Ocena prawdziwości obydwu zdań.
Zdanie pierwsze jest prawdą, bo faktycznie suma dwóch kątów ostrych daje \(90°\), bo \(45°+45°=90°\).
Drugie zdanie jest także prawdą, bowiem \(135°:45°=3\).