Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro okręgi są przystające to znaczy, że mamy tak naprawdę dwa identyczne okręgi (o tej samej długości promienia). Zaznaczając w układzie współrzędnych dane z treści zadania otrzymamy następującą sytuację:
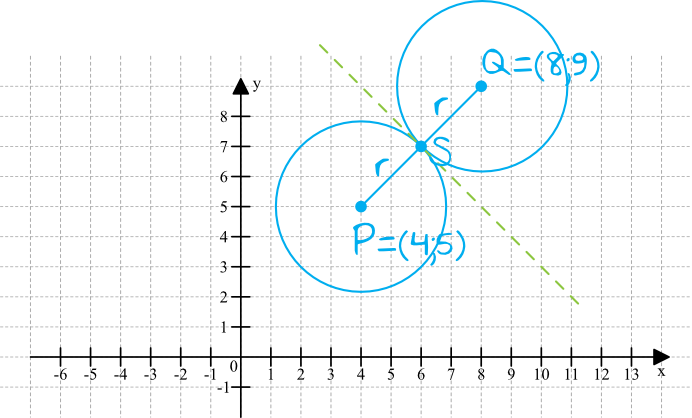
Krok 2. Wyznaczenie środka odcinka \(PQ\).
Skoro okręgi są przystające to punkt styczności \(S\) jest środkiem odcinka \(PQ\), bo \(PS=r\) oraz \(SQ=r\). Za chwilę współrzędne tego punktu przydadzą nam się do dalszych obliczeń, zatem już teraz możemy sobie wyznaczyć jego współrzędne, korzystając ze wzoru dostępnego w tablicach matematycznych:
$$S=\left(\frac{x_{P}+x_{Q}}{2};\frac{y_{P}+y_{Q}}{2}\right) \\
S=\left(\frac{4+8}{2};\frac{5+9}{2}\right) \\
S=\left(\frac{12}{2};\frac{14}{2}\right) \\
S=(6;7)$$
Krok 3. Wyznaczenie współczynnika kierunkowego prostej \(PQ\).
Za chwilę będziemy poszukiwać równania prostej prostopadłej do prostej \(PQ\), zatem przyda nam się znajomość współczynnika kierunkowego prostej \(PQ\). Oczywiście możemy wyznaczyć sobie całe równanie prostej \(PQ\) (np. metodą układu równań), ale nam tak naprawdę potrzebny będzie tylko ten współczynnik kierunkowy, który obliczymy ze wzoru:
$$a=\frac{y_{Q}-y_{P}}{x_{Q}-x_{P}} \\
a=\frac{9-5}{8-4} \\
a=\frac{4}{4} \\
a=1$$
Krok 4. Wyznaczenie równania osi symetrii.
Oś symetrii zapiszemy w postaci kierunkowej \(y=ax+b\). Ustalmy najpierw jaki jest współczynnik kierunkowy \(a\) tej prostej. Jest to prosta prostopadła do prostej \(PQ\), a aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Skoro więc prosta \(PQ\) ma \(a=1\), to oś symetrii musi mieć ten współczynnik równy \(-1\), bo \(-1\cdot1=-1\). Wiemy już zatem, że oś symetrii będzie wyrażać się równaniem \(y=-1x+b\), czyli \(y=-x+b\). Do ustalenia pozostał nam jeszcze współczynnik \(b\), a jego wartość poznamy podstawiając współrzędne punktu \(S=(6;7)\), przez który ta oś przechodzi:
$$y=-x+b \\
7=-6+b \\
b=13$$
To oznacza, że oś symetrii możemy opisać równaniem \(y=-x+13\).