Rozwiązanie
Teoretycznie moglibyśmy rozwiązać tę nierowność obliczając klasyczną deltę, ale jesteśmy w stanie to zadanie zrobić nieco szybciej stosując wzory skróconego mnożenia. W ostateczności nawet możemy podstawiać kolejne liczby z odpowiedzi i sprawdzić kiedy zajdzie opisywana nierówność.
Krok 1. Zapisanie i rozwiązanie nierówności w postaci iloczynowej.
$$x^2\ge9 \\
x^2-9\ge0 \\
(x+3)(x-3)\ge0$$
Z postaci iloczynowej błyskawicznie odczytujemy, że miejscami zerowymi tej nierówności są \(x=-3\) oraz \(x=3\).
Krok 2. Szkicowanie wykresu paraboli.
Znając miejsca zerowe możemy narysować parabolę z ramionami skierowanymi do góry (bo przed \(x^2\) nie stoi żadna ujemna liczba), pamiętając że przy \(-3\) oraz \(3\) kropki będą zamalowane.
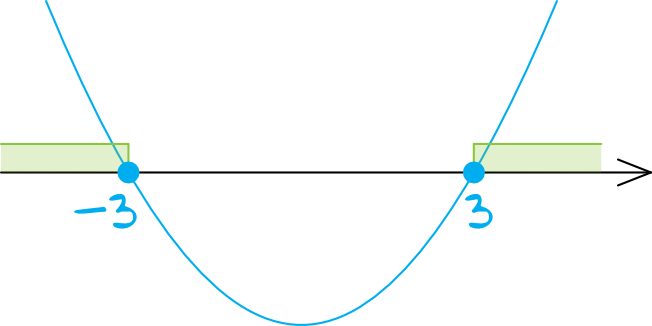
Krok 3. Odczytanie rozwiązania.
Patrzymy w których miejscach funkcja przyjmuje wartości większe od zera, czyli dla jakich przedziałów wykres znalazł się nad osią. W ten sposób możemy stwierdzić, że \(x\in(-\infty;-3\rangle\cup\langle3;+\infty)\).
Spośród wszystkich odpowiedzi tylko \(-3\) mieści się w naszej sumie przedziałów i to właśnie jest poszukiwana odpowiedź.