Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
W sześciokącie foremnym wszystkie kąty wewnętrzne mają miarę \(120°\). Wykorzystując własności kątów możemy sobie narysować następujący szkic:
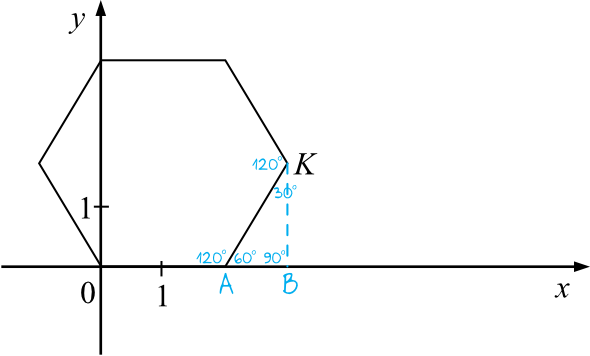
Wiemy, że kąt \(BAK\) ma miarę \(60°\), bo jest to kąt przyległy do kąta \(120°\), a suma miar kątów przyległych jest równa \(180°\). To z kolei oznacza, że powstał nam klasyczny trójkąt o mierze kątów \(30°, 60°, 90°\) z którego własności musimy teraz skorzystać, aby obliczyć długość odcinka \(AB\). To pozwoli nam powiedzieć jak szeroki jest cały sześciokąt.
Krok 2. Wyznaczenie długości odcinka \(AB\).
Zgodnie z własnościami trójkątów \(30°, 60°, 90°\) możemy zapisać, że długość odcinka \(AB\) jest dwa razy krótsza od długości przeciwprostokątnej, czyli:
$$|AB|=2:2=1$$
Krok 3. Wyznaczenie szerokości sześciokąta.
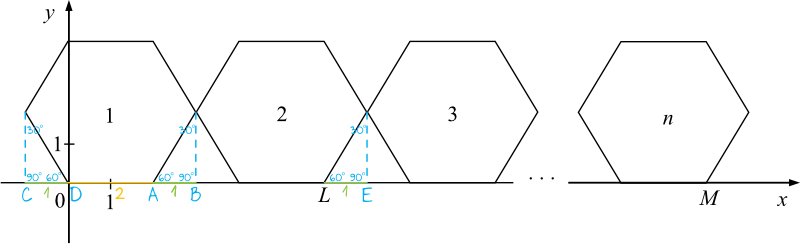
Patrząc na rysunek możemy powiedzieć, że szerokość naszego sześciokąta to długość podstawy plus długości odcinków \(CD\) oraz \(AB\). Odcinek \(CD\) jest równy odcinkowi \(AB\), więc możemy zapisać że szerokość sześciokąta (czyli odcinek \(CB\)) wynosi:
$$1+2+1=4$$
Krok 4. Wyznaczenie pierwszej współrzędnej wierzchołka \(L\) i ocena prawdziwości pierwszego zdania.
Wróćmy do naszego rysunku szkicowego i spróbujmy ustalić jaka jest pierwsza współrzędna wierzchołka \(L\). To będzie tak naprawdę odcinek o długości dwóch szerokości sześciokątów, pomniejszony o odcinki \(CD\) oraz \(LE\). W związku z tym możemy zapisać, że pierwsza współrzędna wierzchołka \(L\) jest równa:
$$4\cdot2-2=6$$
Tym samym wiemy już, że pierwsze zdanie jest prawdą.
Krok 5. Wyznaczenie wzoru na pierwszą współrzędną wierzchołka \(M\) i ocena prawdziwości drugiego zdania.
W poprzednim kroku wyznaczyliśmy pierwszą współrzędną prawej części dolnej podstawy drugiego sześciokąta. Teraz musimy ustalić jaka będzie ta współrzędna nie dla drugiego sześciokąta, a dla \(n\)-tego. Co to zmieni w naszych obliczeniach? Tak jak przed chwilą mnożyliśmy szerokość sześciokąta przez \(2\) (bo mieliśmy drugi sześciokąt), tak teraz musimy pomnożyć go przez \(n\) (bo mamy \(n\)-ty sześciokąt). To oznacza, że wartość tej współrzędnej będzie wyrażać się wzorem:
$$4\cdot n-2$$
To oznacza, że drugie zdanie jest prawdą.