Rozwiązanie
Krok 1. Obliczenie pola podstawy.
W podstawie ostrosłupa mamy kwadrat o boku \(6\), zatem jego pole będzie równe:
$$P_{p}=6\cdot6=36$$
Krok 2. Obliczenie pola powierzchni całkowitej.
Z treści zadania wynika, że pole powierzchni całkowitej jest cztery razy większe od pola powierzchni podstawy, zatem to pole musi być równe:
$$P_{c}=4\cdot P_{p} \\
P_{c}=4\cdot36 \\
P_{c}=144$$
Krok 3. Obliczenie pola pojedynczej ściany bocznej.
Skoro pole powierzchni całkowitej jest równe \(144\), a pole podstawy jest równe \(36\), to pole wszystkich czterech ścian bocznych będzie równe:
$$P_{b}=P_{c}-P_{p} \\
P_{b}=144-36 \\
P_{b}=108$$
My takich ścian mamy cztery, zatem każda z nich (np. ściana \(BCS\)) ma pole powierzchni równe:
$$P_{BCS}=108:4 \\
P_{BCS}=27$$
Krok 4. Obliczenie wysokości ściany bocznej.
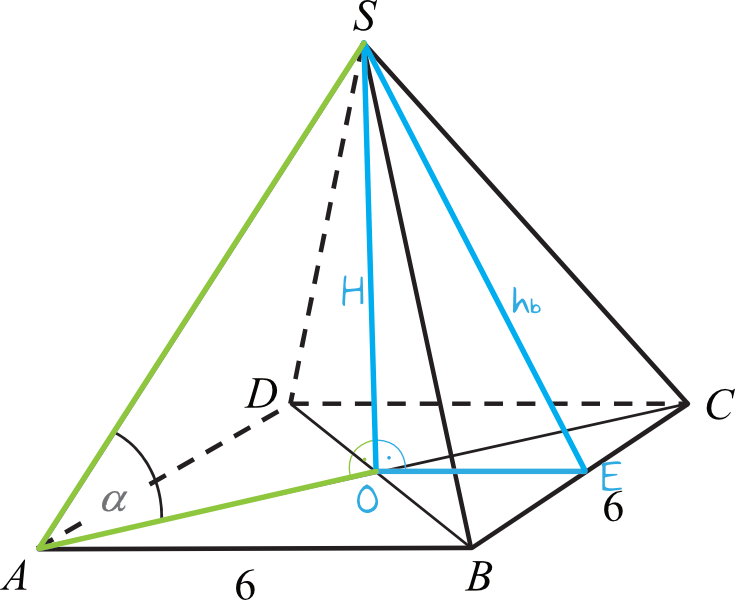
Spójrzmy na jedną ze ścian bocznych, np. na trójkąt \(BCS\). Jest to trójkąt o podstawie równej \(6\) i polu powierzchni równym \(27\). W związku z tym w prosty sposób możemy wyznaczyć wysokość tego trójkąta:
$$P=\frac{1}{2}ah_{b} \\
27=\frac{1}{2}\cdot6\cdot h_{b} \\
54=6h_{b} \\
h_{b}=9$$
Krok 5. Obliczenie wysokości ostrosłupa.
Spójrzmy na niebieski trójkąt \(SOE\). Odcinek \(OE\) to będzie długość równa połowie krawędzi podstawy, czyli:
$$|OE|=6:2 \\
|OE|=3$$
Wiemy też, że \(SE\) ma długość \(9\). Jedynym niewiadomym bokiem w tym trójkącie jest więc odcinek \(SO\), czyli wysokość ostrosłupa. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$H^2+3^2=9^2 \\
H^2+9=81 \\
H^2=72 \\
H=6\sqrt{2}$$
Krok 6. Obliczenie długości krawędzi bocznej.
Spójrzmy na trójkąt \(AOS\) i obliczmy długość krawędzi bocznej \(AS\). Odcinek \(AO\) to połowa długości przekątnej podstawy. Skoro mamy kwadrat o boku \(6\), to cała przekątna ma długość \(6\sqrt{2}\), czyli:
$$|AO|=6\sqrt{2}:2 \\
|AO|=3\sqrt{2}$$
Odcinek \(SO\) (czyli wysokość trójkąta) jest już nam znana, zatem ponownie korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$(3\sqrt{2})^2+(6\sqrt{2})^2=|AS|^2 \\
9\cdot2+36\cdot2=|AS|^2 \\
18+72=|AS|^2 \\
|AS|^2=90 \\
|AS|=\sqrt{90}=3\sqrt{10}$$
Krok 7. Obliczenie cosinusa kąta alfa.
Znając długość odcinka \(AO\) oraz \(AS\) bez problemu obliczymy cosinus kąta alfa:
$$cosα=\frac{|AO|}{|AS|} \\
cosα=\frac{3\sqrt{2}}{3\sqrt{10}} \\
cosα=\frac{\sqrt{2}}{\sqrt{10}} \\
cosα=\frac{\sqrt{2}}{\sqrt{2}\cdot\sqrt{5}} \\
cosα=\frac{1}{\sqrt{5}} \\
cosα=\frac{1\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} \\
cosα=\frac{\sqrt{5}}{5}$$