Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
W tym zadaniu musimy zauważyć, że dorysowując wysokość padającą na bok \(CA\) utworzy nam się tak naprawdę połowa trójkąta równobocznego. Wszystko wyjaśni poniższy rysunek:
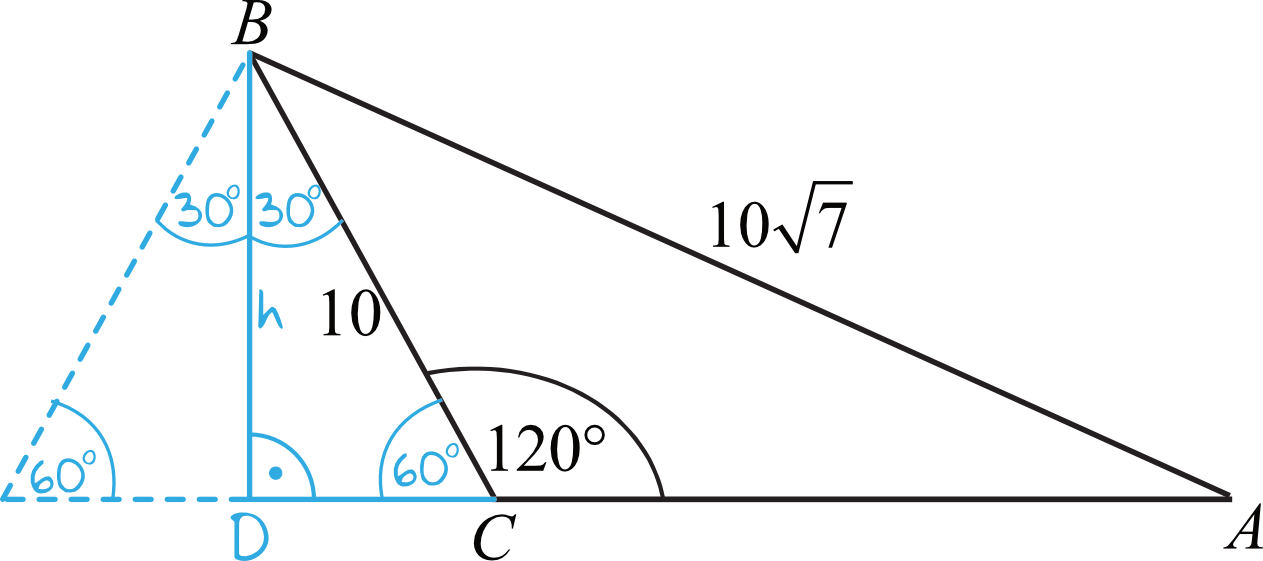
Kąt \(DCB\) ma na pewno miarę \(60°\), gdyż jest to kąt przyległy do kąta \(120°\), a suma kątów przyległych musi być równa \(180°\).
Krok 2. Obliczenie wysokości \(BD\).
Wysokość trójkąta równobocznego obliczymy korzystając ze wzoru:
$$h=\frac{a\sqrt{3}}{2}$$
Wiemy, że bok naszego trójkąta równobocznego ma długość \(a=10\), bo odcinek \(|BC|=10\). Zatem:
$$h=\frac{10\sqrt{3}}{2} \\
h=5\sqrt{3}$$
Krok 3. Obliczenie długości \(DA\).
Spójrzmy teraz na trójkąt \(DAB\). Jest to trójkąt prostokątny w którym znamy długości dwóch boków: \(BD=5\sqrt{3}\) oraz \(|AB|=10\sqrt{7}\). Korzystając zatem z Twierdzenia Pitagorasa obliczymy długość odcinka \(DA\):
$$|BD|^2+|DA|^2=|AB|^2 \\
(5\sqrt{3})^2+|DA|^2=(10\sqrt{7})^2 \\
25\cdot3+|DA|^2=100\cdot7 \\
75+|DA|^2=700 \\
|DA|^2=625 \\
|DA|=25 \quad\lor\quad |DA|=-25$$
Ujemny wynik tego równania kwadratowego oczywiście odrzucamy, bo długość boku nie może być ujemna. W związku z tym \(|DA|=25\).
Krok 4. Obliczenie długości \(DC\).
Długość \(DC\) zgodnie z własnościami trójkątów równobocznych jest równa połowie długości boku trójkąta (bo wysokość dzieli nam podstawę tego trójkąta na dwie równe części). Stąd też:
$$|DC|=10:2 \\
|DC|=5$$
Krok 5. Obliczenie długości \(CA\).
Wiemy już, że \(|DA|=25\). Wiemy też, że \(|DC|=5\). Różnica tych dwóch długości da nam odpowiedź na to jaką długość ma nasz poszukiwany odcinek \(CA\):
$$|CA|=|DA|-|DC| \\
|CA|=25-5 \\
|CA|=20$$