Rozwiązanie
Krok 1. Obliczenie wysokości trójkąta \(ABC\).
Z własności trójkątów równoramiennych wiemy, że ich wysokość przecina podstawę w połowie jej długości, zatem mamy taką oto sytuację:
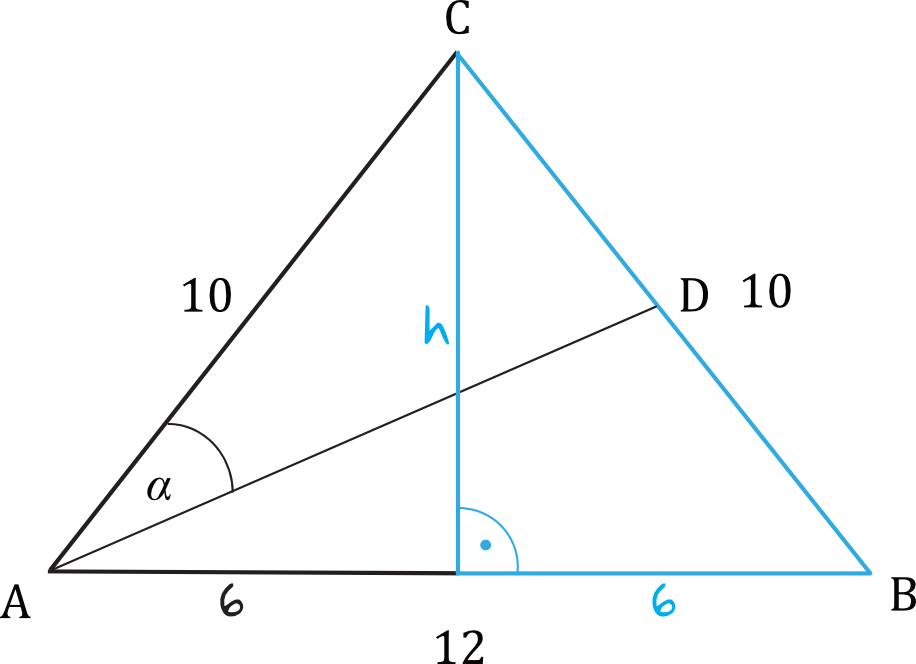
Powstał nam trójkąt prostokątny, w którym jedyną niewiadomą jest wysokość naszego trójkąta \(ABC\), zatem:
$$6^2+H^2=10^2 \\
36+H^2=100 \\
H^2=64 \\
H=8 \quad\lor\quad H=-8$$
Ujemną długość oczywiście odrzucamy, zatem zostaje nam \(H=8\).
Krok 2. Obliczenie pola trójkąta \(ABC\).
Skoro podstawa trójkąta ma długość \(a=12\), a wysokość to \(H=8\), to pole tego trójkąta jest równe:
$$P=\frac{1}{2}\cdot12\cdot8 \\
P=6\cdot8 \\
P=48$$
Krok 3. Obliczenie wysokości trójkąta, która pada na ramię trójkąta.
Spróbujmy teraz obliczyć długość wysokości trójkąta, która pada nie na podstawę, tylko na ramię. Pole powierzchni jest już nam znane, wiemy że \(P=48\). W tym przypadku podstawa będzie miała długość ramienia, czyli \(a=10\), zatem:
$$P=\frac{1}{2}\cdot a\cdot h \\
48=\frac{1}{2}\cdot10\cdot h \\
48=5\cdot h \\
h=9,6$$
Krok 4. Sporządzenie rysunku pomocniczego.
Mamy w tym momencie taką oto sytuację:
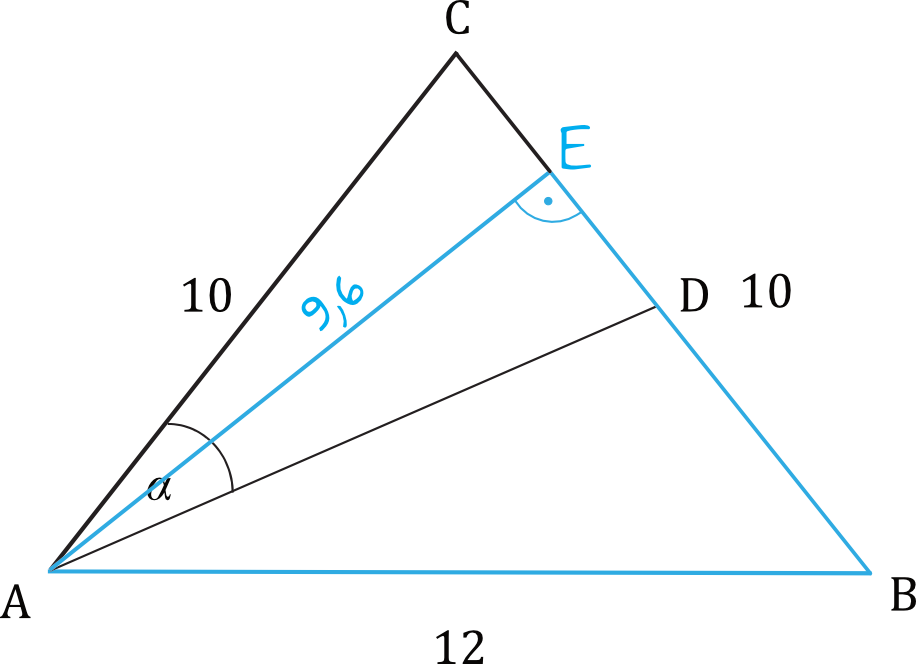
Krok 5. Obliczenie długości odcinka \(EB\).
Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$|EB|^2+9,6^2=12^2 \\
|EB|^2+92,16=144 \\
|EB|^2=51,84 \\
|EB|=7,2 \quad\lor\quad |EB|=-7,2$$
Długość odcinka nie może być ujemna, więc zostaje nam \(|EB|=7,2\).
Krok 6. Obliczenie długości odcinka \(ED\).
Długość odcinka \(ED\) jest różnicą między długością odcinka \(EB\) oraz \(DB\), zatem:
$$|ED|=7,2-5 \\
|ED|=2,2$$
Krok 7. Obliczenie długości odcinka \(AD\).
Ponownie skorzystamy z Twierdzenia Pitagorasa, tym razem w trójkącie \(AED\):
$$9,6^2+2,2^2=|AD|^2 \\
92,16+4,84=|AD|^2 \\
|AD|^2=97 \\
|AD|=\sqrt{97} \quad\lor\quad |AD|=-\sqrt{97}$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(|AD|=\sqrt{97}\).
Krok 8. Obliczenie wartości \(sin\alpha\).
Spoglądamy teraz na trójkąt \(ADC\). Jego pole powierzchni jest równe:
$$P=\frac{1}{2}\cdot5\cdot9,6 \\
P=24$$
Wiedząc jakie jest pole tego trójkąta oraz znając długości odcinków \(AC\) oraz \(AD\), możemy teraz obliczyć poszukiwaną wartość \(sin\alpha\). W tym celu musimy skorzystać z tak zwanego wzoru na pole powierzchni trójkąta "z sinusem":
$$P=\frac{1}{2}ab\cdot sin\alpha \\
24=\frac{1}{2}\cdot10\cdot\sqrt{97}\cdot sin\alpha \\
24=5\sqrt{97}\cdot sin\alpha \\
sin\alpha=\frac{24}{5\sqrt{97}}=\frac{24\cdot\sqrt{97}}{5\sqrt{97}\cdot\sqrt{97}}=\frac{24\sqrt{97}}{5\cdot97}=\frac{24\sqrt{97}}{485}$$