Dany jest trójkąt równoramienny ABC, w którym AC=BC oraz A=(2,1) i C=(1,9)

Dany jest trójkąt równoramienny $ABC$, w którym $|AC|=|BC|$ oraz $A=(2,1)$ i $C=(1,9)$. Podstawa $AB$ tego trójkąta jest zawarta w prostej $y=\frac{1}{2}x$. Oblicz współrzędne wierzchołka $B$.

Rozwiązanie:

Krok 1. Sporządzenie rysunku poglądowego.

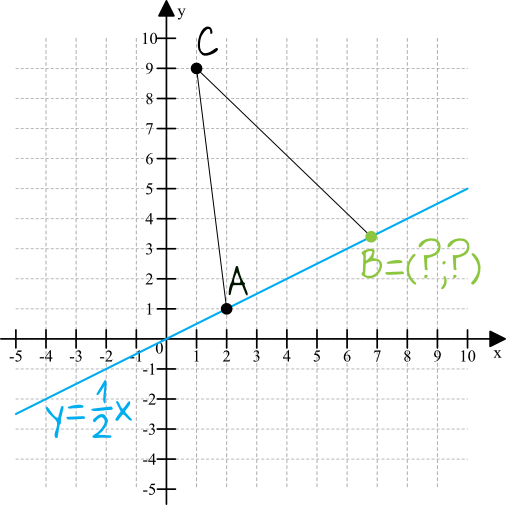
Nasz rysunek możemy wykonać dość dokładnie, dzięki czemu będziemy w stanie zweryfikować później poprawność naszych obliczeń.

Krok 2. Określenie współrzędnych punktu $B$.

Współrzędne każdego punktu możemy określić jako $(x;y)$. Z treści zadania wiemy, że przez punkt $B$ przechodzi prosta o równaniu $y=\frac{1}{2}x$. Możemy więc podstawić wartość tego „igreka” za współrzędną $y$ i zapisać współrzędne tego punktu jako: $B=(x;\frac{1}{2}x)$.

Dzięki temu pozbyliśmy się niewiadomej $y$, a to nam znacznie ułatwi dotarcie do końcowego rozwiązania.

Krok 3. Zapisanie równania wynikającego z trójkąta równoramiennego.

Skorzystamy ze wzorów na długość odcinków w układzie współrzędnych. Wiemy, że boki $AC$ oraz $BC$ mają tą samą długość, dlatego między miarami tych odcinków możemy postawić znak równości. Znamy współrzędne $A$ i $C$, zapisaliśmy też sobie współrzędne punktu $B$ z wykorzystaniem jednej niewiadomej, zatem:
$$|AC|=|BC| \\
\sqrt{(x_{C}-x_{A})^2+(y_{C}-y_{A})^2}=\sqrt{(x_{C}-x_{B})^2+(y_{C}-y_{B})^2} \\
(1-2)^2+(9-1)^2=(1-x)^2+\left(9-\frac{x}{2}\right)^2 \\
1+64=1-2x+x^2+81-9x+\frac{x^2}{4} \\
65=x^2+\frac{1}{4}x^2-11x+82 \\
\frac{5}{4}x^2-11x+17=0 \quad\bigg/\cdot4 \\
5x^2-44x+68=0$$

Krok 4. Rozwiązanie powstałego równania kwadratowego.

Współczynniki: $a=5,\;b=-44,\;c=68$
$$Δ=b^2-4ac=(-44)^2-4\cdot5\cdot68=1936-1360=576 \\
\sqrt{Δ}=\sqrt{576}=24$$

$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-44)-24}{2\cdot5}=\frac{44-24}{10}=\frac{20}{10}=2 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-44)+24}{2\cdot5}=\frac{44+24}{10}=\frac{68}{10}$$

Krok 5. Analiza otrzymanych rozwiązań i określenie końcowych współrzędnych punktu $B$.

Dla $x=2$ otrzymaliśmy współrzędną punktu $A$. To nie jest więc to rozwiązanie, które nas interesuje, choć też jest dla nas ważne, bo przy okazji potwierdza poprawność naszych obliczeń (wszak punkt $A$ także leży na prostej $y=\frac{1}{2}x$).

Współrzędne punktu $B$ otrzymaliśmy z drugiego rozwiązania, czyli $x=\frac{68}{10}$. Brakuje nam jeszcze współrzędnej $y$, ale zgodnie z tym co zapisaliśmy sobie w drugim kroku i zgodnie z równaniem prostej przechodzącej przez ten punkt:
$$y=\frac{1}{2}x \\
y=\frac{1}{2}\cdot\frac{68}{10} \\
y=\frac{68}{20}$$

Otrzymane wyniki możemy jeszcze skrócić i wyłączyć z nich całość, tak więc:
$$x=\frac{68}{10}=6\frac{4}{5} \\
y=\frac{68}{20}=3\frac{2}{5}$$

Poszukiwane współrzędne to $B=\left(6\frac{4}{5};3\frac{2}{5}\right)$.

Odpowiedź:

$B=\left(6\frac{4}{5};3\frac{2}{5}\right)$

Zadania

Dany jest trójkąt równoramienny ABC, w którym AC=BC oraz A=(2,1) i C=(1,9)

Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\) oraz \(A=(2,1)\) i \(C=(1,9)\). Podstawa \(AB\) tego trójkąta jest zawarta w prostej \(y=\frac{1}{2}x\). Oblicz współrzędne wierzchołka \(B\).