Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Jedną z własności stycznych do okręgu jest to, że promień okręgu tworzy ze styczną kąt prosty. To oznacza, że na rysunku powstanie nam taka oto sytuacja:
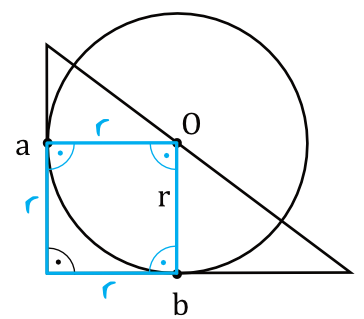
Co więcej, możemy w takim razie podpisać dwa odcinki jako \(a-r\) oraz \(b-r\):
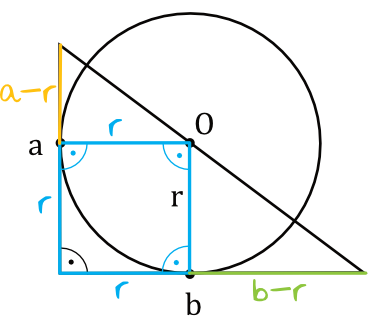
Krok 2. Dostrzeżenie trójkątów podobnych.
Powinniśmy teraz zauważyć, że na rysunku mamy tak naprawdę dwa podobne trójkąty prostokątne. Skąd wiemy, że są one podobne? Wynika to z cechy kąt-kąt-kąt (obydwa mają kąt prosty, obydwa mają wspólny kąt ostry między bokiem \(b\) oraz przeciwprostokątną, zatem i trzecia miara kątów musi być wspólna).
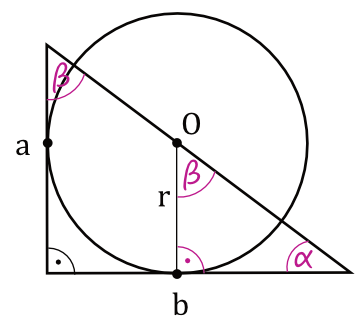
Krok 3. Wykorzystanie cech podobieństwa trójkątów.
Korzystając z cech trójkątów podobnych możemy zapisać, że stosunek długości przyprostokątnych jednego trójkąta musi być taki sam, jak stosunek długości przyprostokątnych drugiego trójkąta, zatem:
$$\frac{a}{b}=\frac{r}{b-r}$$
Długości boków są zawsze dodatnie, więc bez obaw możemy teraz wykonać mnożenie na krzyż:
$$a\cdot(b-r)=br \\
ab-ar=br \\
ab=ar+br \\
ab=r(a+b) \\
r=\frac{ab}{a+b}$$
Otrzymaliśmy pożądaną postać, zatem dowodzenie możemy uznać za zakończone.