Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania będzie wyglądać następująco:
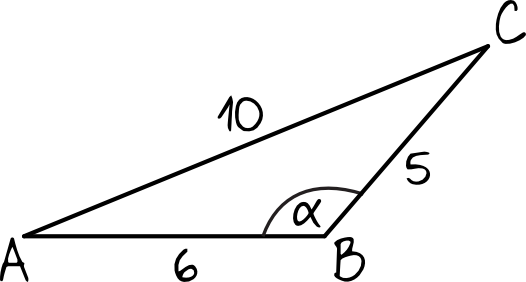
Krok 2. Ocena prawdziwości pierwszego zdania.
Korzystając z twierdzenia cosinusów możemy zapisać, że:
$$10^2=6^2+5^2-2\cdot6\cdot5\cdot cos\alpha \\
100=36+25-60cos\alpha \\
100=61-60cos\alpha \\
39=-60cos\alpha \\
cos\alpha=-0,65$$
Zdanie jest więc prawdą.
Krok 3. Ocena prawdziwości drugiego zdania.
Z twierdzenia odwrotnego do twierdzenia Pitagorasa wiemy, że gdy \(a^2+b^2=c^2\), to trójkąt jest prostokątny. Rozwinięciem tego twierdzenia jest informacja, że jeżeli \(a^2+b^2\gt c^2\), to trójkąt jest ostrokątny, natomiast gdy \(a^2+b^2\lt c^2\), to trójkąt jest rozwartokątny. W naszym przypadku \(a=6\), \(b=5\) oraz \(c=10\), zatem:
$$a^2+b^2=6^2+5^2=36+25=61 \\
c^2=10^2=100$$
Widzimy więc, że \(a^2+b^2\) jest mniejsze od \(c^2\), zatem jest to trójkąt rozwartokątny. Zdanie jest więc prawdą.