Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
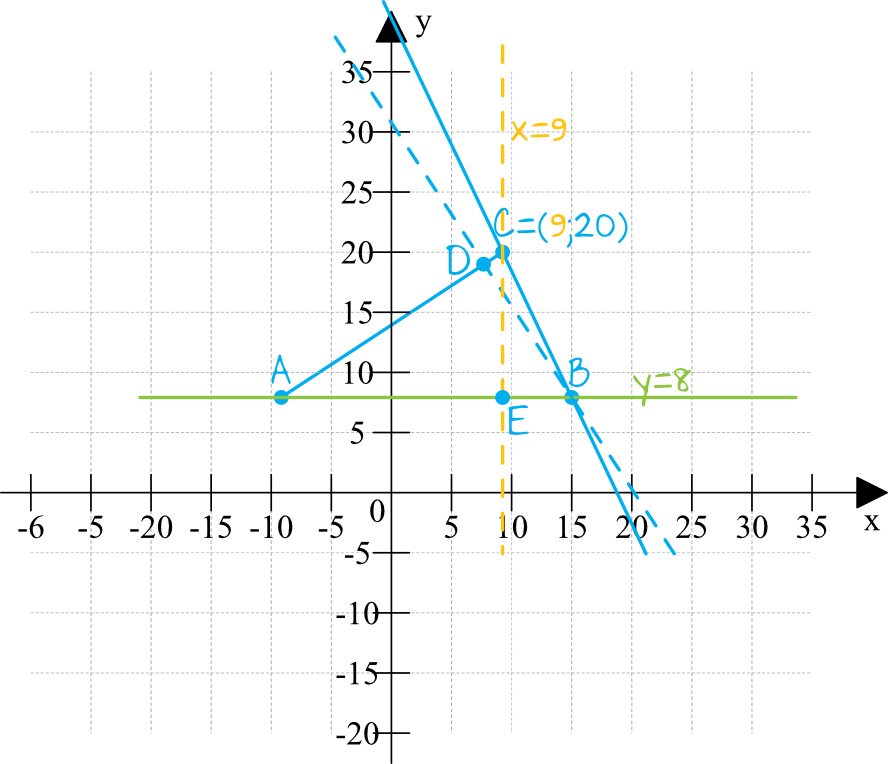
Narysujmy sobie szkic całej sytuacji, tak aby mieć lepszy podgląd na to co trzeba zrobić:
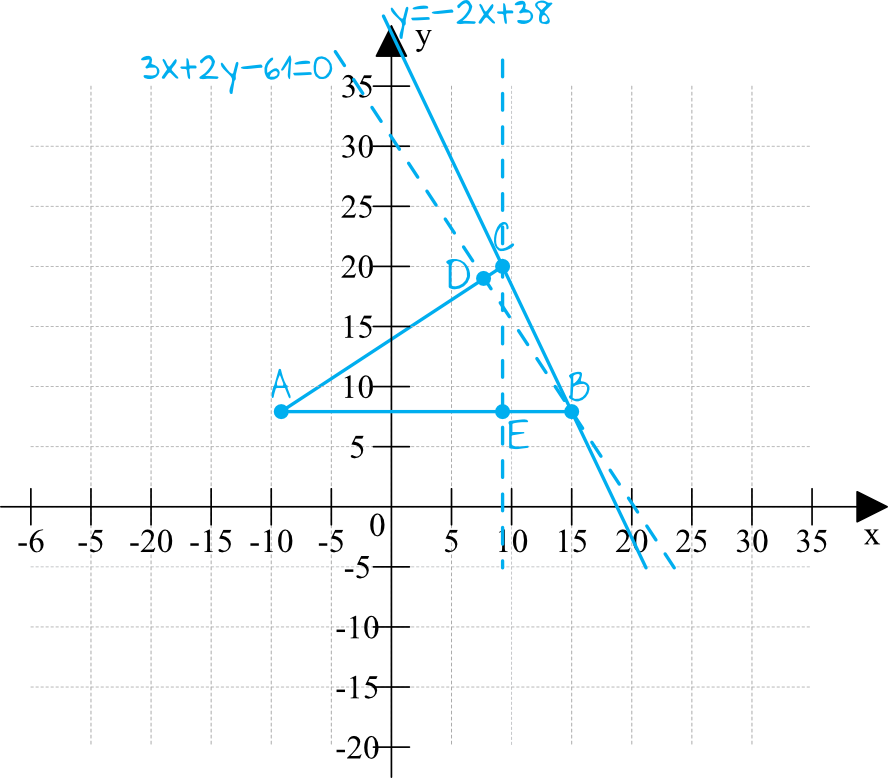
Liniami przerywanymi zostały narysowane wysokości opuszczone z wierzchołka \(B\) oraz \(C\).
Krok 2. Wyznaczenie współrzędnych punktu \(B\).
Z treści zadania (i tym samym z rysunku) wynika, że proste o równaniu \(y=-2x+38\) oraz \(3x+2y-61=0\) przecinają się w punkcie \(B\). Zgodnie z tak zwaną geometryczną interpretacją układu równań wiemy, że rozwiązaniem układu równań zbudowanego z dwóch prostych będzie miejsce ich przecięcia. W ten sposób będziemy mogli wyznaczyć współrzędne punktu \(B\), zatem:
$$\begin{cases}
y=-2x+38 \\
3x+2y-61=0
\end{cases}$$
Podstawiając pierwsze równanie do drugiego otrzymamy:
$$3x+2\cdot(-2x+38)-61=0 \\
3x-4x+76-61=0 \\
-x+15=0 \\
x=15$$
Znając wartość iksa możemy teraz obliczyć wartość igreka, podstawiając do dowolnego z równań (np. pierwszego) wartość \(x=15\):
$$y=-2x+38 \\
y=-2\cdot15+38 \\
y=-30+38 \\
y=8$$
To oznacza, że \(B=(15,8)\).
Krok 3. Zapisanie równania prostej \(BD\) w postaci kierunkowej.
Prosta \(BD\) będąca wysokością poprowadzoną z wierzchołka \(B\) jest zapisana w postaci ogólnej, a my za chwilę będziemy potrzebować postaci kierunkowej (do wyznaczenia prostej prostopadłej). W związku z tym już teraz przekształćmy ten zapis do wspomnianej postaci kierunkowej:
$$3x+2y-61=0 \\
2y=-3x+61 \\
y=-\frac{3}{2}x+30\frac{1}{2}$$
Krok 4. Wyznaczenie równania prostej \(AC\).
Wiemy, że prosta \(AC\) jest prostopadła do prostej \(BD\). Z własności prostych prostopadłych wynika, że aby dwie proste były względem prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Prosta \(BD\) ma współczynnik kierunkowy równy \(a=-\frac{3}{2}\), zatem prosta \(AC\), czyli prosta prostopadła, będzie mieć ten współczynnik równy \(a=\frac{2}{3}\), bo \(-\frac{3}{2}\cdot\frac{2}{3}=-1\). To oznacza, że prosta \(AC\) wyraża się równaniem \(y=\frac{2}{3}x+b\). Brakuje nam jeszcze wartości współczynnika \(b\), a poznamy go podstawiając do tego równania współrzędne punktu \(A\), czyli \(x=-9\) oraz \(y=8\):
$$y=\frac{2}{3}x+b \\
8=\frac{2}{3}\cdot(-9)+b \\
8=-6+b \\
b=14$$
Skoro współczynnik \(b=14\) to prosta \(AC\) wyraża się równaniem \(y=\frac{2}{3}x+14\).
Krok 5. Wyznaczenie współrzędnej punktu \(C\).
Zastosujemy identyczny zabieg co przy wyznaczaniu współrzędnych punktu \(B\). Punkt \(C\) jest miejscem przecięcia się prostych \(y=-2x+38\) oraz \(y=\frac{2}{3}x+14\), zatem jego współrzędne obliczymy rozwiązując następujący układ równań:
\begin{cases}
y=-2x+38 \\
y=\frac{2}{3}x+14
\end{cases}
Podstawiając pierwsze równanie do drugiego otrzymamy:
$$-2x+38=\frac{2}{3}x+14 \quad\bigg/\cdot3 \\
-6x+114=2x+42 \\
-8x=-72 \\
x=9$$
Znając wartość iksa możemy teraz obliczyć wartość igreka, podstawiając do dowolnego z równań (np. pierwszego) wartość \(x=9\):
$$y=-2x+38 \\
y=-2\cdot9+38 \\
y=-18+38 \\
y=20$$
To oznacza, że \(C=(9,20)\).
Krok 6. Wyznaczenie równania prostej \(CE\).
Poszukiwana przez nas prosta \(CE\) (czyli wysokość opuszczona z wierzchołka \(C\)) jest prostopadła do prostej \(AB\). Teoretycznie powinniśmy najpierw obliczyć jakie jest równanie prostej \(AB\), a potem obliczyć równanie prostej \(CE\), ale da się poznać wzór tej prostej znacznie szybciej.
Powinniśmy zauważyć, że punkty \(A\) i \(B\) mają jednakową współrzędną igrekową, czyli leżą "na tej samej linii". Bez żadnych więc obliczeń możemy zapisać, że prosta \(AB\) wyraża się równaniem \(y=8\). Prostymi prostopadłymi do tej prostej byłyby więc np. \(x=1\), \(x=3\) czy też \(x=7\). Nas interesuje taka prosta prostopadła, która przejdzie przez punkt \(C=(9,20)\), czyli przejdzie przez współrzędną iksową równą \(9\). Z tego też względu interesująca nas prosta \(CE\) wyrazi się wzorem \(x=9\).