Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Stwórzmy sobie prosty rysunek na którym zaznaczymy to co nas interesuje, czyli odległości punktów \(A\) i \(B\) od prostej \(CS\). Przypomnę, że odległość punktu od prostej to tak naprawdę odcinek, który jest prostopadły do wskazanej prostej.
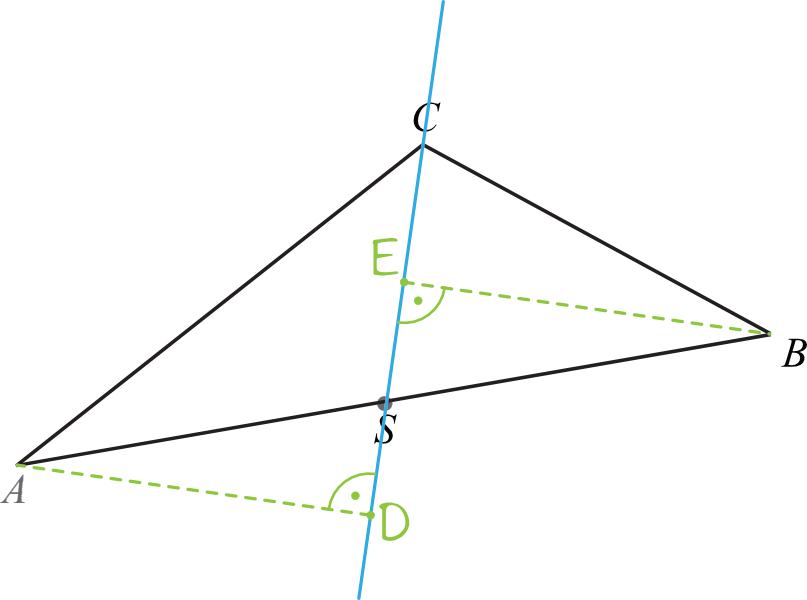
Krok 2. Dostrzeżenie przystawania trójkątów.
Spójrzmy na trójkąty \(ADS\) oraz \(SBE\). Naszym zadaniem jest teraz udowodnić, że te trójkąty są trójkątami przystającymi (nie wystarczy by były podobne, muszą być przystające, czyli muszą mieć jednakowe miary poszczególnych boków). Jak udowodnimy, że są to trójkąty przystające, to będziemy mieć pewność że przyprostokątne tych trójkątów (czyli odcinki łączące punkty z prostą \(CS\) zaznaczone przerywaną zieloną linią) mają jednakowe miary.
Przeanalizujmy zatem te dwa trójkąty. Są to trójkąty prostokątne, czyli już na pewno wiemy, że mają jedną wspólną miarę kątów. Dodatkowo kąty przy wierzchołku \(S\), czyli \(ASD\) oraz \(ESB\) są kątami wierzchołkowymi, zatem te kąty także mają jednakową miarę.
Aby udowodnić, że te trójkąty są przystające (czyli jednakowe) to musimy jeszcze wykazać, że mają przynajmniej jedną parę boków równej długości (cecha kąt-bok-kąt). Skoro punkt \(S\) jest środkiem boku \(AB\), to znaczy że przeciwprostokątne \(AS\) oraz \(SB\) mają tą samą miarę, a to pozwala nam stwierdzić, że te trójkąty są na pewno przystające, a tym samym odcinki \(AD\) oraz \(EB\) są jednakowej miary.