Dany jest trójkąt \(ABC\). Odcinek \(CD\) jest wysokością tego trójkąta, punkt \(E\) jest środkiem boku \(BC\) (tak jak na rysunku) i \(|CD|=|DE|\). Udowodnij, że trójkąt \(CDE\) jest równoboczny.
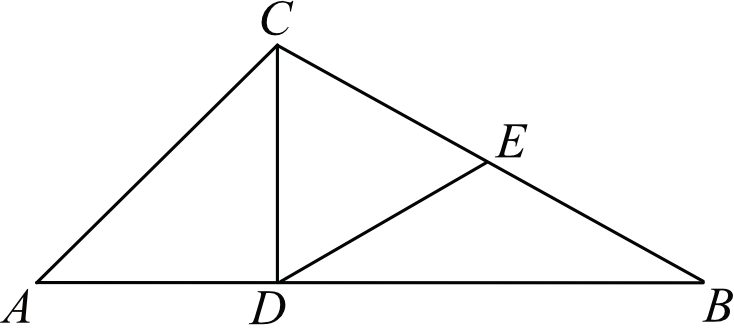
Wiedząc, że punkt \(E\) przecina odcinek \(BC\) na dwie równe części możemy z tego punktu narysować okrąg oparty na trójkącie prostokątnym \(DBC\).

Z własności trójkąta prostokątnego opisanego na okręgu wynika, że przeciwprostokątna trójkąta jest równa długości średnicy okręgu, a tym samym odcinki \(CE\) oraz \(EB\) mają długość równą długości promienia (patrz rysunek). Jeśli przypatrzymy się rysunkowi, to zobaczymy że także odcinek \(DE\) ma długość równą promieniowi (bo jest to odcinek od krawędzi okręgu do środka okręgu. Zatem wiemy już na pewno, że \(|CE|=|DE|=r\).
W treści zadania mamy podaną informację o tym, że \(|CD|=|DE|\), a skoro tak, to rzeczywiście trójkąt \(CDE\) jest równoboczny, a długość jego wszystkich boków jest równa długości promienia okręgu opisanego na trójkącie \(DBC\).
Udowodniono opisując trójkąt \(DBC\) na okręgu.

