Dany jest trójkąt ABC o bokach długości 6, 7 oraz 8

Dany jest trójkąt $ABC$ o bokach długości $6$, $7$ oraz $8$. Oblicz cosinus największego kąta tego trójkąta.

Rozwiązanie

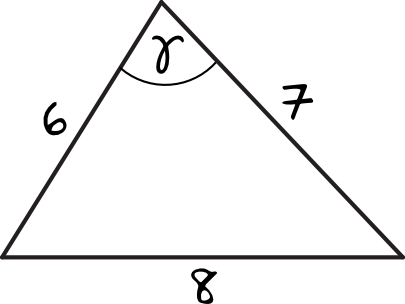
matura z matematyki
Kąt o największej mierze będą tworzyć dwa najkrótsze boki, które możemy oznaczyć jako $a=6$ oraz $b=7$. Najdłuższy bok będzie leżał naprzeciwko tego kąta, czyli $c=8$. Mając te dane, możemy teraz skorzystać z twierdzenia cosinusów, zatem:
$$8^2=6^2+7^2-2\cdot6\cdot7\cdot cos\gamma \\
64=36+49-84cos\gamma \\
64=85-84cos\gamma \\
-21=-84cos\gamma \\
cos\gamma=\frac{1}{4}$$

Odpowiedź

$cos\gamma=\frac{1}{4}$

Zadania

Dany jest trójkąt ABC o bokach długości 6, 7 oraz 8

Dany jest trójkąt \(ABC\) o bokach długości \(6\), \(7\) oraz \(8\). Oblicz cosinus największego kąta tego trójkąta.