Rozwiązanie
Krok 1. Ocena prawdziwości pierwszego zdania.
Trójkąt \(KLN\) jest trójkątem prostokątnym w którym znamy już miary dwóch kątów: \(26°\) oraz \(90°\). Musimy ustalić teraz jaka jest miara trzeciego kąta, czyli kąta \(NKL\), zatem:
$$|\sphericalangle NKL|=180°-90°-26°=64°$$
To oznacza, że zdanie jest prawdą.
Krok 2. Ocena prawdziwości drugiego zdania.
Korzystając z własności kątów naprzemianległych powinniśmy dostrzec, że kąty \(KLN\) oraz \(LNM\) będą miały jednakową miarę, czyli kąt \(LNM\) będzie miał także \(26°\).
Na kąt \(KNM\) składają się dwa kąty: \(KNL\) oraz \(LNM\). Skoro kąt \(KNL\) ma miarę \(90°\), to kąt \(LNM\) ma miarę:
$$|\sphericalangle LNM|=116°-90°=26°$$
Z treści zadania wynika, że trójkąt \(NLM\) jest równoramienny (bo boki \(LM\) oraz \(MN\) są sobie równe). Trójkąty równoramienne mają jednakową miarę kąta przy swojej podstawie. To by oznaczało, że w takim razie kąt \(NLM\) ma także miarę \(26°\).
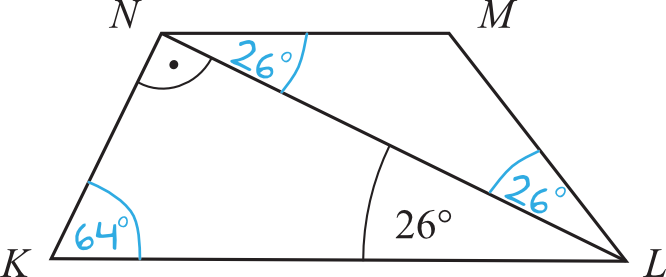
Skoro tak, to kąt \(KLM\), na który składają się kąty \(KLN\) oraz \(NLM\) będzie miał miarę:
$$|\sphericalangle KLM|=26°+26°=52°$$
Wiemy już zatem, że kąt \(NKL\) ma miarę \(64°\), natomiast \(KLM\) ma miarę \(52°\). W trapezach równoramiennych kąty przy podstawie muszą mieć jednakową miarę, a tu widzimy że tak się nie stało. To oznacza, że ten trapez nie jest równoramienny.