Dany jest trapez ABCD, w którym AB||CD oraz przekątne AC i BD przecinają się w punkcie O

Dany jest trapez $ABCD$, w którym $AB||CD$ oraz przekątne $AC$ i $BD$ przecinają się w punkcie $O$ (zobacz rysunek). Wysokość tego trapezu jest równa $12$. Obwód trójkąta $ABO$ jest równy $39$, a obwód trójkąta $CDO$ jest równy $13$.

Wysokość trójkąta $ABO$ poprowadzona z punktu $O$ jest równa:

A. $3$

B. $4$

C. $9$

D. $6$

Rozwiązanie

Krok 1. Dostrzeżenie trójkątów podobnych.
Z własności trapezów wynika, że trójkąty $ABO$ oraz $CDO$ są trójkątami podobnymi (wynika to z cechy kąt-kąt-kąt, ponieważ kąty tych trójkątów przy wierzchołku $O$ są kątami wierzchołkowymi, a kąty przy podstawach są kątami naprzemianległymi). Dobrze to widać na tym rysunku:
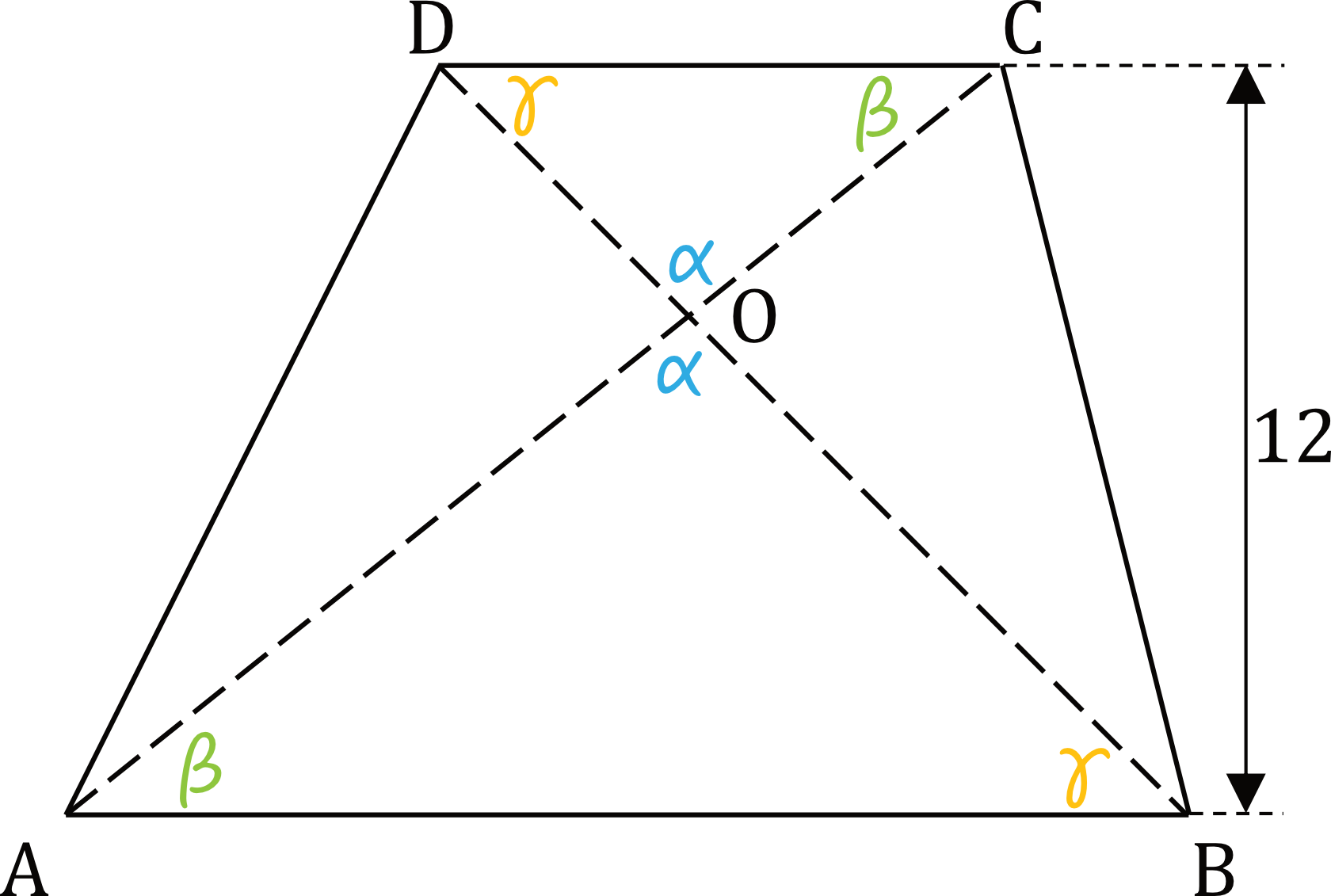
matura z matematyki

Krok 2. Obliczenie skali podobieństwa.
Skoro nasze trójkąty są podobne, to na podstawie informacji o obwodach tych trójkątów, możemy obliczyć skalę podobieństwa. Jeżeli przyjmiemy, że trójkąt $ABO$ jest trójkątem podstawowym, a $CDO$ jest trójkątem podobnym, to:
$$k=\frac{39}{13} \\
k=3$$

Krok 3. Obliczenie wysokości trójkąta $ABO$.
Skoro skala podobieństwa tych trójkątów jest równa $3$, to analogicznie wysokość trójkąta $ABO$ jest $3$ razy większa od wysokości trójkąta $CDO$. Powstaje nam więc taka oto sytuacja:
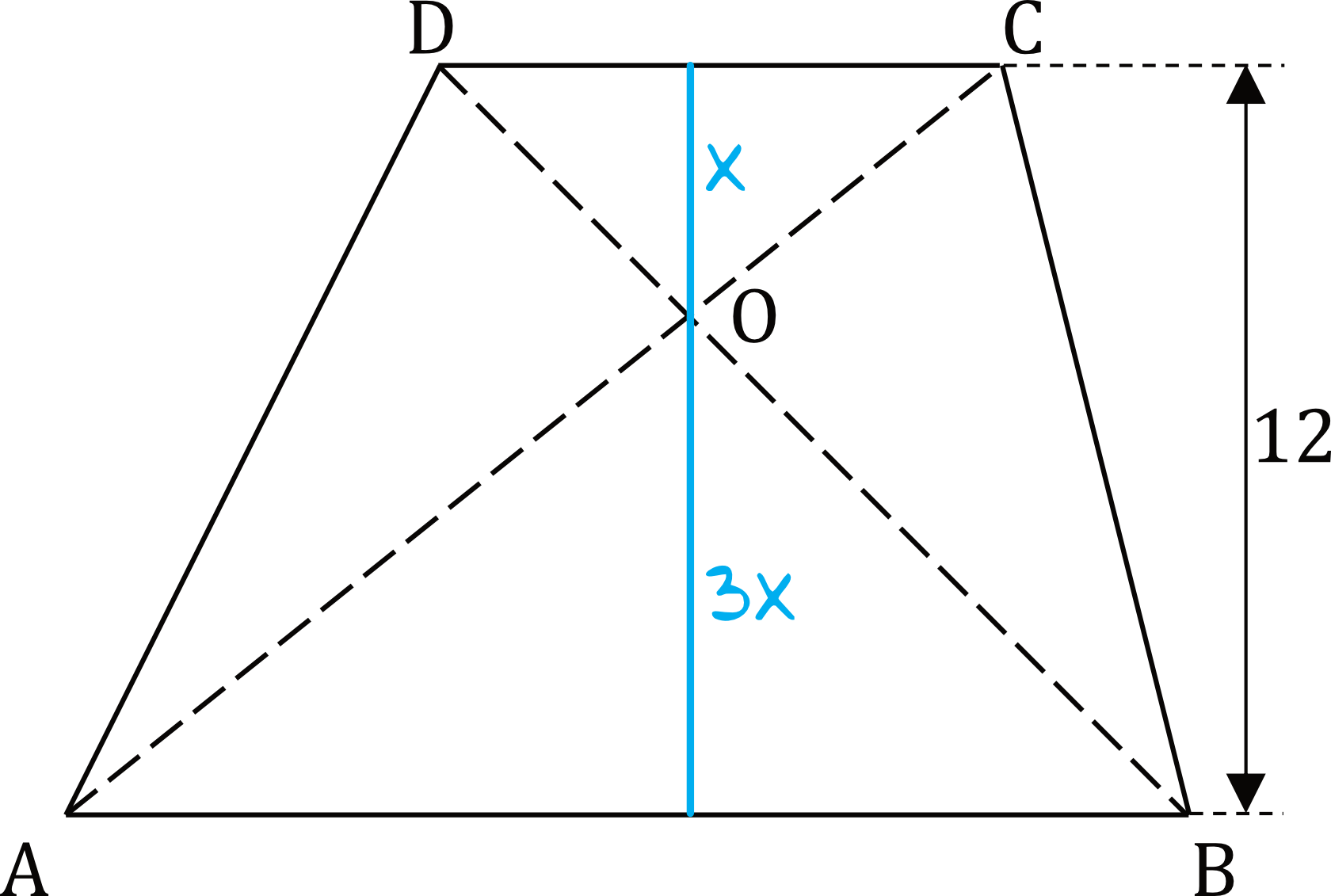
matura z matematyki

Wiemy, że suma długości tych wysokości jest równa $12$, zatem:
$$x+3x=12 \\
4x=12 \\
x=3$$

Trójkąt $ABO$ ma wysokość $3x$, zatem:
$$h=3\cdot3=9$$

Odpowiedź