Dany jest sześcian \(ABCDEFGH\). Siatką ostrosłupa czworokątnego \(ABCDE\) jest:
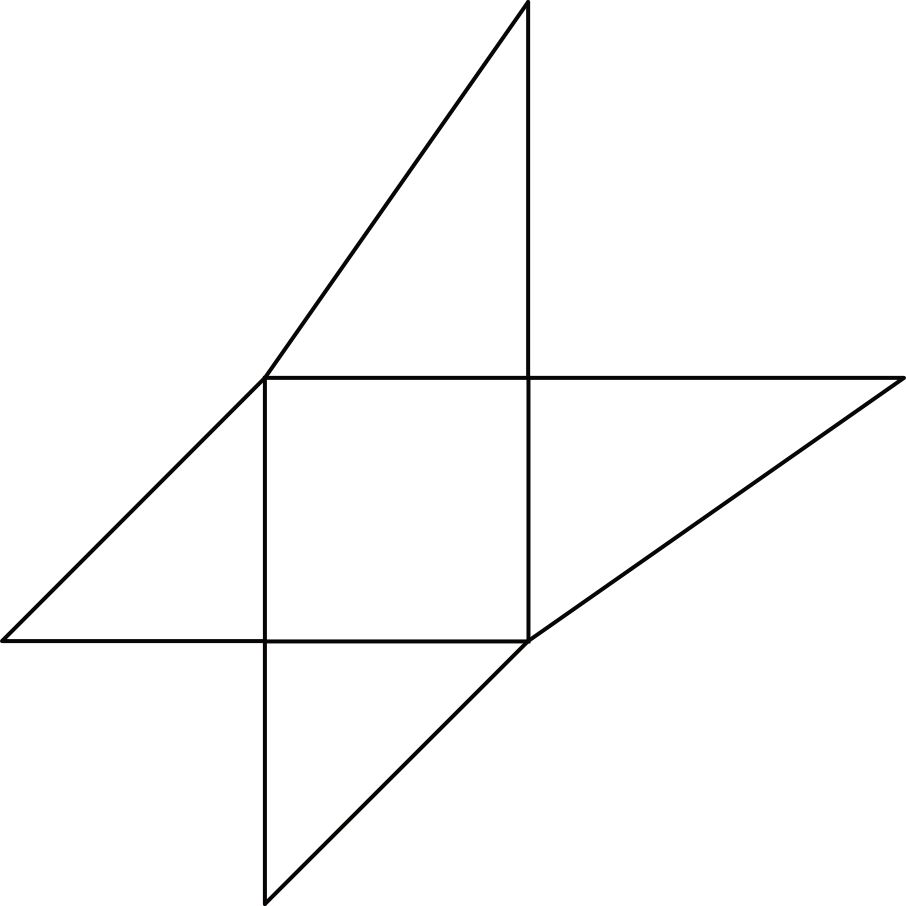
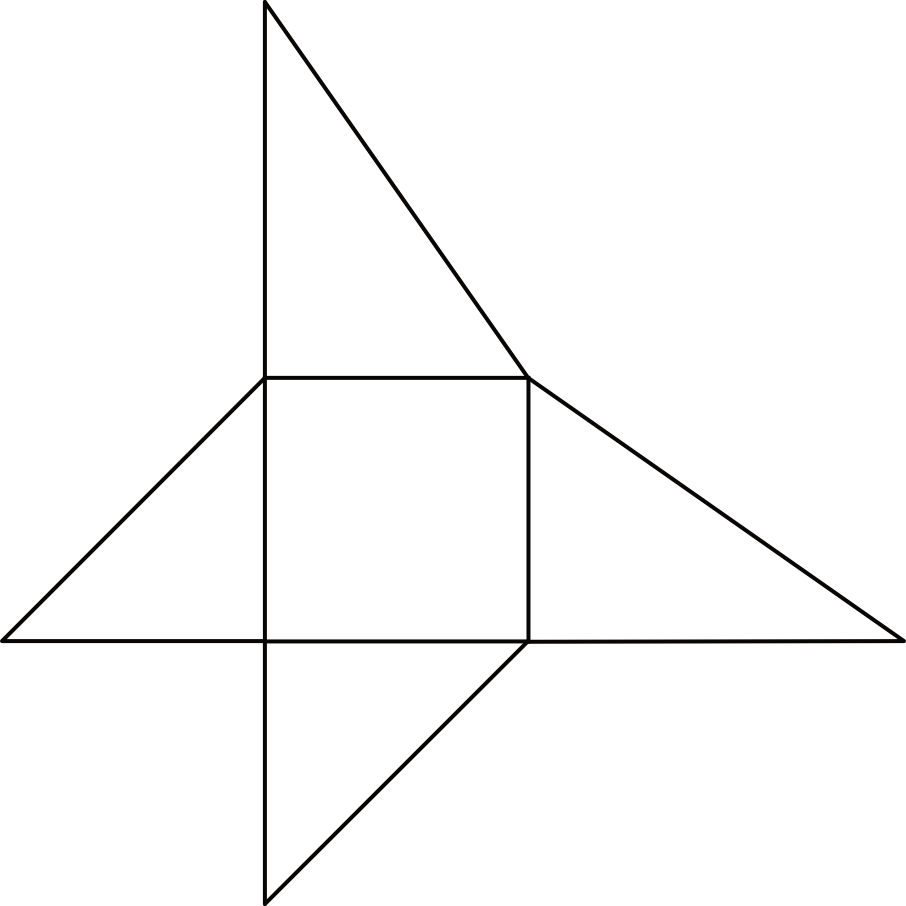
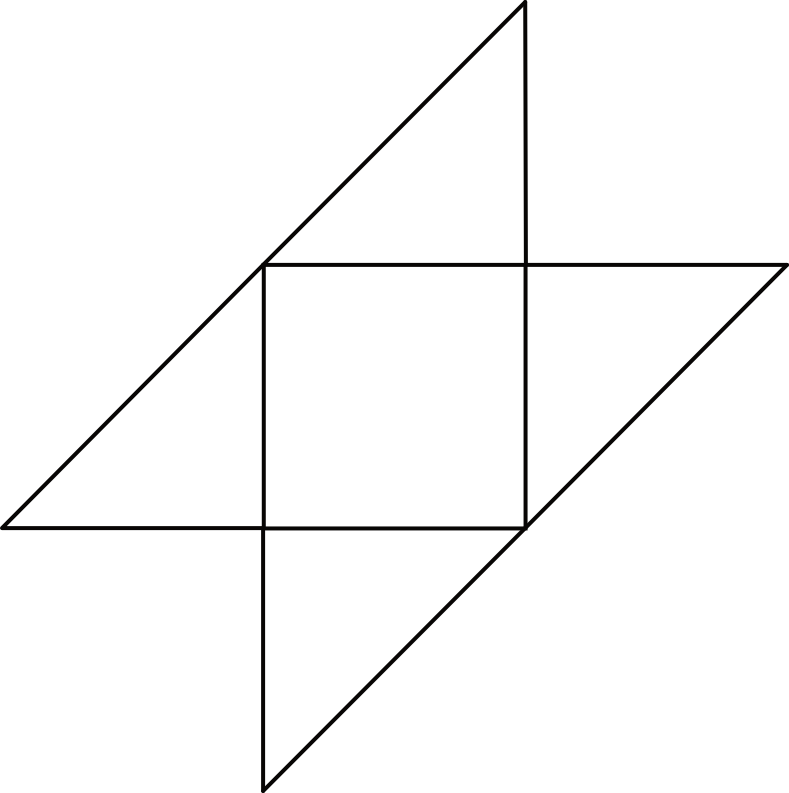
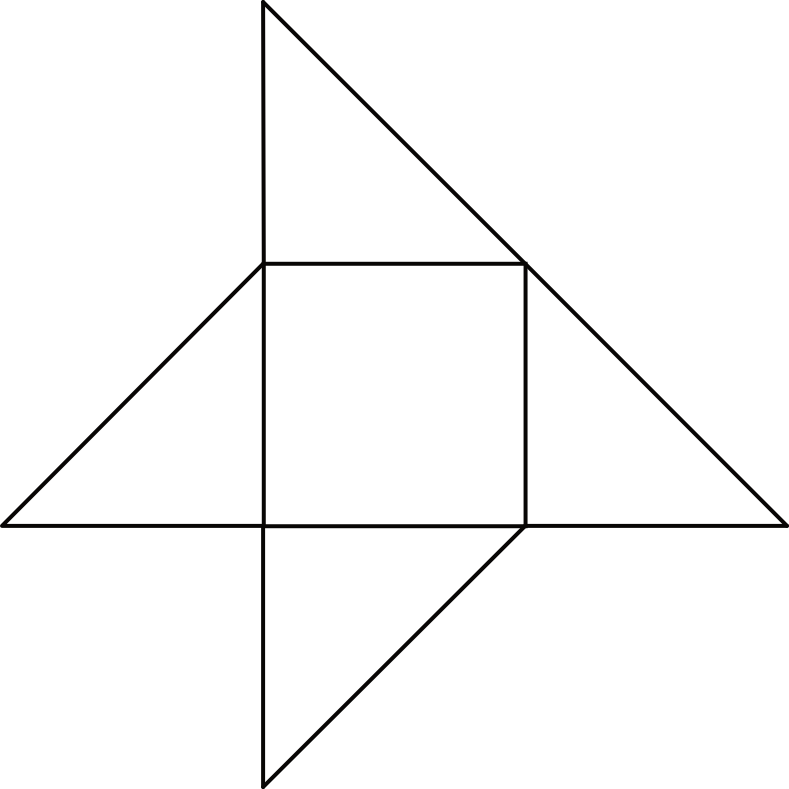
W naszej siatce powinniśmy się spodziewać dwóch różnych rodzajów trójkątów. Pierwszym rodzajem są trójkąty \(ABE\) oraz \(ADE\) (są na pewno prostokątne i równoramienne bo wyznacza nam to bok sześcianu). Drugim rodzajem są trójkąty \(BCE\) oraz \(CDE\) (też będą to trójkąty prostokątne, ale już nie będą równoramienne no i będą tak jakby „dłuższe”).
Już ta pierwsza weryfikacja sprawia, że odrzucimy odpowiedzi \(C\) i \(D\), bo tam wszystkie trójkąty są jednakowych rozmiarów. Teraz używając naszej wyobraźni przestrzennej musimy dokonać wyboru między \(A\) i \(B\). Siatka \(A\) różni się od \(B\) jedynie ułożeniem dwóch „dłuższych” trójkątów. W siatce \(B\) najdłuższe krawędzie wychodzą z jednego wierzchołka i to jest dla nas znak, że po złożeniu te krawędzie idealnie się ze sobą spasują. W siatce \(A\) już takiej zależności nie znajdziemy i w zasadzie po złożeniu tej siatki otrzymamy bardzo nieregularną figurę przestrzenną (nie będzie nam nawet to przypominać ostrosłupa). Stąd też prawidłowa jest odpowiedź \(B\).


