Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanosząc dane z treści zadania otrzymamy następującą sytuację:
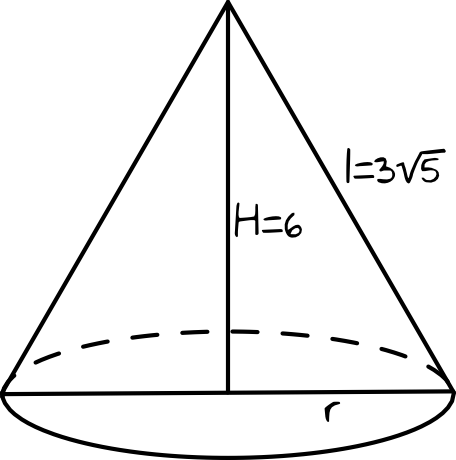
Krok 2. Obliczenie długości promienia podstawy.
Do objętości potrzebna nam jest znajomość promienia podstawy, a tę wyliczymy z Twierdzenia Pitagorasa:
$$r^2+h^2=l^2 \\
r^2+6^2=(3\sqrt{5})^2 \\
r^2+36=9\cdot5 \\
r^2+36=45 \\
r^2=9 \\
r=3 \quad\lor\quad r=-3$$
Ujemne rozwiązanie odrzucamy, bo promień musi mieć dodatnią długość, zatem \(r=3\).
Krok 3. Obliczenie objętości stożka.
Mamy już wszystkie potrzebne miary, zatem podstawiając do wzoru na objętość stożka otrzymamy:
$$V=\frac{1}{3}P_{p}\cdot h \\
V=\frac{1}{3}πr^2\cdot h \\
V=\frac{1}{3}π\cdot3^2\cdot6 \\
V=\frac{1}{3}π\cdot9\cdot6 \\
V=3π\cdot6 \\
V=18π$$