Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro w przekroju stożka mamy trójkąt prostokątny, to zajdzie taka oto sytuacja:
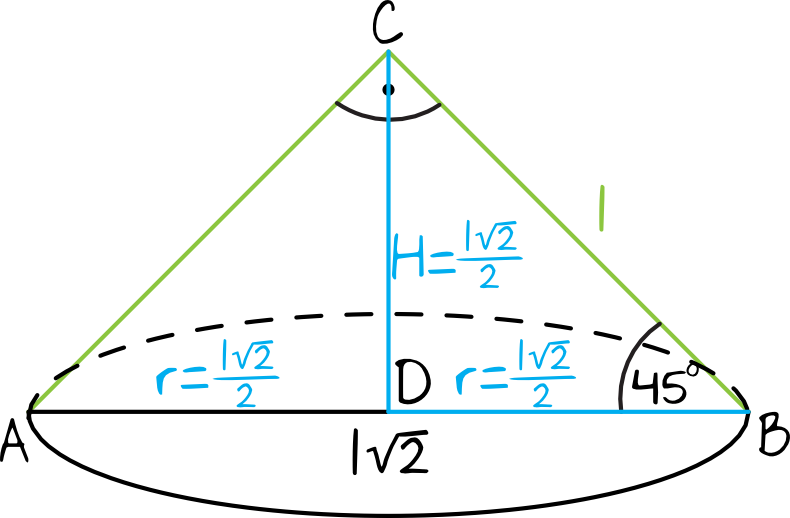
Ustalmy jeszcze skąd wzięły się takie, a nie inne oznaczenia i miary. Wiemy, że trójkąt jest prostokątny i że jest równoramienny (bo zawsze w przekroju stożka mamy trójkąt równoramienny o ramieniu długości \(l\)). Z własności trójkątów wynika, że każdy trójkąt prostokątny równoramienny jest trójkątem o kątach \(45°, 45°, 90°\). Dostrzeżenie tego faktu jest kluczem do całości zadania.
Skoro przyprostokątne trójkąta \(ABC\) są równe \(l\) to przeciwprostokątna (czyli w tym przypadku podstawa \(AB\) i jednocześnie średnica okręgu w podstawie) jest równa \(l\sqrt{2}\). Wiemy też średnica jest dwukrotnie większa od promienia, czyli \(r=\frac{l\sqrt{2}}{2}\).
Skąd natomiast wiadomo, że wysokość stożka jest równa \(h=\frac{l\sqrt{2}}{2}\)? Tutaj musimy spojrzeć chociażby na trójkąt \(DBC\). To także jest trójkąt o kątach \(45°, 45°, 90°\), a jego przyprostokątnymi są właśnie promień okręgu i wysokość bryły. Te dwie długości zgodnie z własnościami takich trójkątów muszą być sobie równe, stąd też skoro \(r=\frac{l\sqrt{2}}{2}\), to także \(h=\frac{l\sqrt{2}}{2}\).
Krok 2. Obliczenie długości tworzącej stożka \(l\).
Podstawiając wszystkie dane do wzoru na objętość otrzymamy:
$$V=\frac{1}{3}P_{p}\cdot h \\
V=\frac{1}{3}\pi\cdot r^2\cdot h \\
18π\sqrt{2}=\frac{1}{3}\pi\cdot\left(\frac{l\sqrt{2}}{2}\right)^2\cdot\frac{l\sqrt{2}}{2} \\
18π\sqrt{2}=\frac{1}{3}\pi\cdot\frac{2l^2}{4}\cdot\frac{l\sqrt{2}}{2} \\
18\sqrt{2}=\frac{1}{3}\cdot\frac{l^2}{2}\cdot\frac{l\sqrt{2}}{2} \\
18\sqrt{2}=\frac{l^2\cdot l\sqrt{2}}{12} \\
216\sqrt{2}=l^3\sqrt{2} \\
l^3=216 \\
l=6$$
Krok 3. Obliczenie długości promienia oraz wysokości bryły.
Znając długość tworzącej stożka bardzo szybko możemy obliczyć także pozostałe kluczowe długości w tej bryle:
$$r=\frac{l\sqrt{2}}{2}=\frac{6\sqrt{2}}{2}=3\sqrt{2} \\
h=\frac{l\sqrt{2}}{2}=\frac{6\sqrt{2}}{2}=3\sqrt{2}$$
Krok 4. Obliczenie pola powierzchni całkowitej.
Znamy już wszystkie niezbędne miary, zatem możemy przystąpić do obliczenia pola powierzchni całkowitej stożka:
$$P_{c}=P_{p}+P_{b} \\
P_{c}=πr^2+πrl \\
P_{c}=π\cdot(3\sqrt{2})^2+π\cdot(3\sqrt{2})\cdot6 \\
P_{c}=π\cdot18+π\cdot18\sqrt{2} \\
P_{c}=18π+18\sqrt{2}π$$
Możemy (ale nie musimy) wyłączyć jeszcze przed nawias \(18π\), otrzymując:
$$P_{c}=18π(1+\sqrt{2}) \\
P_{c}=18π(\sqrt{2}+1)$$