Rozwiązanie
Krok 1. Obliczenie długości odcinków \(KE\) oraz \(EL\).
Spójrzmy na mały trójkąt \(KEN\). Z treści zadania możemy wywnioskować, że odcinki \(NK\) oraz \(NE\) mają długość \(1cm\). Skoro tak, to wiemy już, że jest to trójkąt prostokątny równoramienny, czyli krótko mówiąc - jest to trójkąt o kątach \(45°, 45°, 90°\). W takich trójkątach przeciwprostokątna jest \(\sqrt{2}\) razy większa od długości przyprostokątnych (podobna sytuacja jak z przekątną kwadratu), zatem odcinek \(KE\) ma miarę \(\sqrt{2}cm\). Gdybyśmy o tej własności nie pamiętali, to moglibyśmy wyliczyć długość odcinka \(KE\) z Twierdzenia Pitagorasa.
Teraz spójrzmy na mały trójkąt \(ELM\). Tutaj sytuacja jest identyczna jak przed chwilą, ten trójkąt także ma przyprostokątne o długości \(1cm\), zatem odcinek \(EL\) ma także długość \(\sqrt{2}cm\).
Nanieśmy teraz te nasze informacja na rysunek:
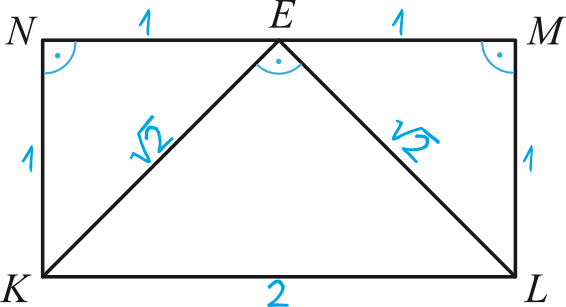
Przy okazji zwróć uwagę na to, że kąt \(KEL\) jest kątem prostym. Skąd to wiemy? Możemy to udowodnić z Twierdzenia Pitagorasa, bowiem zachodzi tutaj równość:
$$(\sqrt{2})^2+(\sqrt{2})^2=2^2 \\
2+2=4 \\
4=4 \\
L=P$$
To oznacza, że trójkąt \(KEL\) jest prostokątny.
Krok 2. Ocena prawdziwości pierwszego zdania.
Aby trójkąty były względem siebie przystające, to muszą mieć jednakowe długości wszystkich boków. Widzimy wyraźnie, że trójkąty \(KEN\) oraz \(KEL\) mają różne miary, więc na pewno nie są przystające. Zdanie jest więc fałszem.
Tak na marginesie - te trójkąty są podobne (a nie przystające) i to jest główna pułapka w tym zadaniu. Skala podobieństwa tych trójkątów będzie równa \(k=\sqrt{2}\), bowiem każdy bok trójkąta \(KEL\) jest \(\sqrt{2}\) razy większy od boku trójkąta \(KEN\).
Krok 3. Ocena prawdziwości drugiego zdania.
Do zadania możemy podejść na dwa sposoby. Jeżeli ustalimy sobie (tak jak w poprzednim kroku), że skala podobieństwa tych trójkątów jest równa \(k=\sqrt{2}\), to bardzo szybko będziemy w stanie ustalić, że pole trójkąta \(KEL\) będzie \(2\) razy większe od pola trójkąta \(MEL\), bowiem \(k^2=\sqrt{2}^2=2\). To będzie więc jednocześnie oznaczało, że faktycznie pole trójkąta \(MEL\) jest dwa razy mniejsze od pola trójkąta \(KEL\).
Jeżeli jednak nie dostrzegliśmy podobieństwa trójkątów, to posłużyć możemy się standardowymi wzorami na pole trójkąta, wszak w trójkątach prostokątnych długości przyprostokątnych są jednocześnie podstawą oraz wysokością. Zatem:
$$P_{MEL}=\frac{1}{2}ah \\
P_{MEL}=\frac{1}{2}\cdot1\cdot1 \\
P_{MEL}=0,5[cm^2]$$
$$P_{KEL}=\frac{1}{2}ah \\
P_{KEL}=\frac{1}{2}\cdot\sqrt{2}\cdot\sqrt{2} \\
P_{KEL}=1[cm^2]$$
Teraz widzimy wyraźnie, że pole trójkąta \(MEL\) jest faktycznie dwa razy mniejsze od pola trójkąta \(KEL\). Zdanie jest więc prawdą.