Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
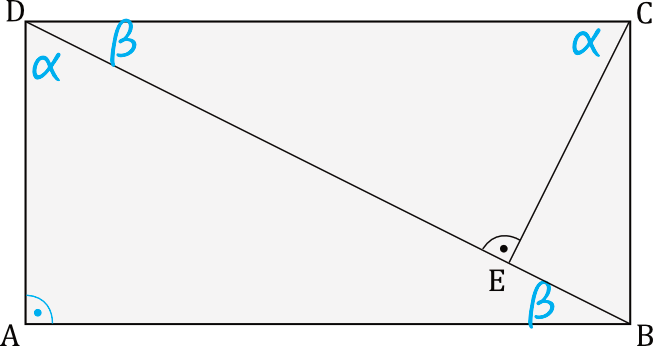
Na początek oznaczmy kąt \(BDA\) jako \(\alpha\) (zgodnie z treścią zadania) oraz \(ABD\) jako \(\beta\). W tym momencie powinniśmy dostrzec, że kąt \(DBC\) jest kątem naprzemianległym do kąta \(ABD\), zatem on też będzie mieć miarę \(\beta\). W tym momencie widzimy, że trójkąty \(ABD\) oraz \(DEC\) mają już dwa kąty o jednakowej mierze (kąt \(\beta\) oraz kąt prosty). To z kolei prowadzi nas do wniosku, że w takim razie kąt \(ECD\) musi mieć miarę \(\alpha\), a więc trójkąty \(ABD\) oraz \(DEC\) są trójkątami podobnymi (cecha kąt-kąt-kąt).
Krok 2. Obliczenie długości odcinków \(AB\) oraz \(CD\).
Z treści zadania wiemy, że \(|AD|=2\). Wiemy też, że \(tg\alpha=2\). Skoro tak, to korzystając z funkcji trygonometrycznych możemy zapisać, że:
$$tg\alpha=\frac{|AB|}{|AD|} \\
2=\frac{|AB|}{2} \\
|AB|=4$$
Wyszło nam, że \(|AB|=4\), a skoro figura \(ABCD\) jest prostokątem to i analogicznie \(|CD|=4\).
Krok 3. Obliczenie długości odcinka \(BD\).
Spójrzmy na trójkąt prostokątny \(ABD\). Znamy długości przyprostokątnych tego trójkąta, zatem do wyznaczenia przeciwprostokątnej \(BD\) możemy wykorzystać Twierdzenie Pitagorasa:
$$2^2+4^2=|BD|^2 \\
4+16=|BD|^2 \\
|BD|^2=20 \\
|BD|=\sqrt{20} \quad\lor\quad |BD|=-\sqrt{20}$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(|BD|=\sqrt{20}\). Teoretycznie moglibyśmy jeszcze wyłączyć czynnik przed znak pierwiastka (otrzymując postać \(|BD|=2\sqrt{5})\), ale na tym etapie nie jest to konieczne.
Krok 4. Obliczenie długości odcinka \(CE\).
Ustaliliśmy już, że trójkąty \(ABD\) oraz \(DEC\) są trójkątami podobnymi. Skoro tak, to:
$$\frac{|AD|}{|BD|}=\frac{|CE|}{|CD|} \\
\frac{2}{\sqrt{20}}=\frac{|CE|}{4} \\
|CE|=\frac{8}{\sqrt{20}} \\
|CE|=\frac{8}{2\sqrt{5}} \\
|CE|=\frac{4}{\sqrt{5}} \\
|CE|=\frac{4\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} \\
|CE|=\frac{4\sqrt{5}}{5}$$