Dany jest prostokąt ABCD. Na boku CD tego prostokąta wybrano taki punkt E, że |EC|=2|DE|

Dany jest prostokąt $ABCD$. Na boku $CD$ tego prostokąta wybrano taki punkt $E$, że $|EC|=2|DE|$, a na boku $AB$ wybrano taki punkt $F$, że $|BF|=|DE|$. Niech $P$ oznacza punkt przecięcia prostej $EF$ z prostą $BC$ (zobacz rysunek). Wykaż, że trójkąty $AED$ i $FPB$ są przystające.

Rozwiązanie

Krok 1. Sporządzenie rysunku pomocniczego.
Wprowadźmy na nasz rysunek pewne oznaczenia. Oznaczmy odcinek $DE$ jako $x$, a co za tym idzie odcinek $EC$ jako $2x$. Z treści zadania wynika, że odcinek $BF$ jest równy odcinkowi $DE$, czyli tutaj także mamy długość $x$. Dodatkowo oznaczmy już inną niewiadomą boki $AD$ oraz $BC$, które mają jednakową miarę (niech to będzie niewiadoma $y$), no i niech kluczowy bok $BP$ ma miarę $z$.

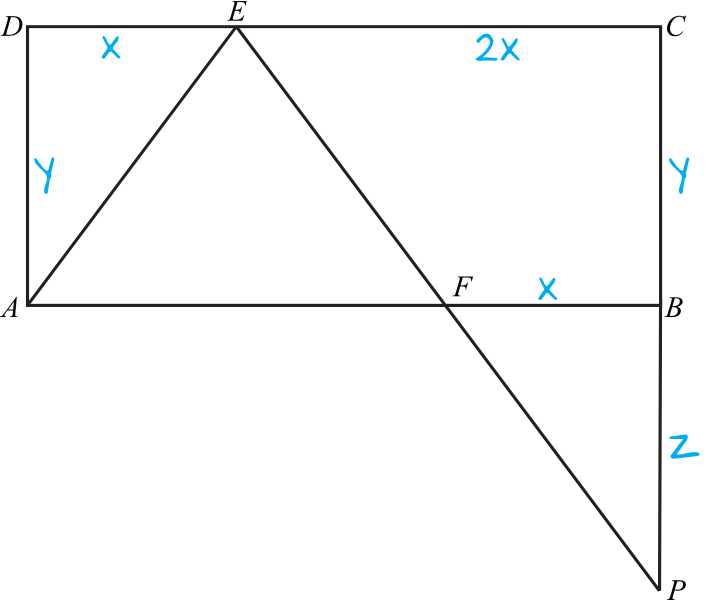
matura z matematyki

Naszym zadaniem jest udowodnienie, że trójkąty $AED$ oraz $FPB$ są przystające, a skoro mają taką samą podstawę równą $x$ to musimy tak naprawdę udowodnić, że $y=z$ (tylko wtedy będą to trójkąty przystające).

Krok 2. Dostrzeżenie podobieństwa trójkątów $PCE$ oraz $PBF$.
Trójkąty $PCE$ oraz $PBF$ są na pewno podobne (mają jednakowe miary kątów). Skoro więc trójkąt $PCE$ ma podstawę równą $2x$, a trójkąt $PBF$ ma podstawę dwukrotnie mniejszą, bo równą $x$, to znaczy że także odcinek $PC$ musi być dwukrotnie dłuższy od odcinka $PB$ (czyli skala podobieństwa jest równa $2$). Zatem:
$$|PC|=2|PB| \\
y+z=2z \quad\bigg/-z \\
y=z$$

Krok 3. Zakończenie dowodzenia.
Udało nam się w ten sposób udowodnić, że długość $y$ jest równa długości $z$. To oznacza, że trójkąty $AED$ oraz $FPB$ mają jednakowe długości przyprostokątnych, zatem i przeciwprostokątne muszą mieć tą samą długość. Skoro więc obydwa trójkąty mają boki jednakowych miar, to są to trójkąty przystające.

Odpowiedź

Wykazano korzystając z podobieństwa trójkątów.