Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
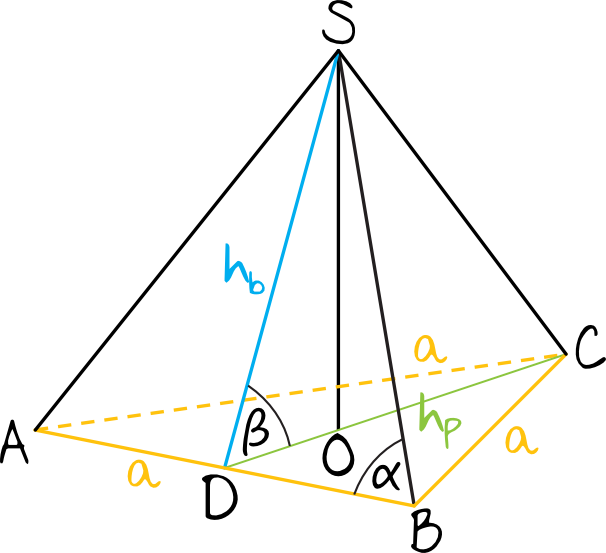
Na początku stwórzmy prosty rysunek pomocniczy, na którym zaznaczymy przede wszystkim kąt \(α\) (co stanowi w sumie jedną z większych pułapek tego zadania, bo zazwyczaj zaznaczamy inne kąty w ostrosłupie niż kąt płaski ściany bocznej) oraz kąt \(β\), który jest kątem nachylenia ściany bocznej ostrosłupa do płaszczyzny podstawy:
Krok 2. Rozpisanie tangensa.
Spójrzmy na trójkąt prostokątny \(DBS\), który utworzył nam się na rysunku pomocniczym. Wiemy, że tangens to stosunek długości przyprostokątnej leżącej naprzeciw kąta \(α\) do długości przyprostokątnej leżącej przy tym kącie. W naszym przypadku otrzymamy więc następujące równanie:
$$tgα=\frac{h_{b}}{\frac{1}{2}a} \\
2=\frac{h_{b}}{\frac{1}{2}a} \quad\bigg/\cdot\frac{1}{2}a \\
a=h_{b}$$
Z naszych obliczeń wynika więc, że wysokość ściany bocznej jest równa długości krawędzi podstawy.
Krok 3. Obliczenie długości krawędzi podstawy.
Skorzystamy teraz z informacji, która mówi że pole powierzchni bocznej tego ostrosłupa jest równe \(24\). W naszym ostrosłupie mamy \(3\) identyczne ściany boczne, zatem pole powierzchni każdej z nich jest równe:
$$P_{b}=24:3=8$$
W ścianie bocznej znajduje się trójkąt o podstawie \(a\) oraz wysokości \(h_{b}\), która jak już ustaliliśmy jest równa długości \(a\), zatem:
$$P=\frac{1}{2}a\cdot h_{b} \\
8=\frac{1}{2}a\cdot a \\
16=a^2 \\
a=4 \quad\lor\quad a=-4$$
Wartość ujemną oczywiście odrzucamy, bo długość nie może być ujemna. W związku z tym \(a=4\) i tym samym \(h_{b}=4\).
Krok 4. Obliczenie wysokości trójkąta znajdującego się w podstawie oraz obliczenie długości odcinka \(AO\).
Spójrzmy teraz na trójkąt prostokątny \(AOS\) z zaznaczonym kątem \(β\). To właśnie cosinus tego kąta musimy wyznaczyć, a do tego niezbędna będzie znajomość odcinka \(AO\). Czym jest ten odcinek \(AO\)? Jest to długość \(\frac{1}{3}\) wysokości trójkąta równobocznego znajdującego się w podstawie (wynika to z własności trójkątów równobocznych). Musimy więc obliczyć wysokość trójkąta równobocznego, korzystając z następującego wzoru:
$$h_{p}=\frac{a\sqrt{3}}{2} \\
h_{p}=\frac{4\sqrt{3}}{2} \\
h_{p}=2\sqrt{3}$$
Odcinek \(AO\) jest zatem równy:
$$|AO|=\frac{1}{3}\cdot2\sqrt{3}=\frac{2\sqrt{3}}{3}$$
Krok 5. Obliczenie wartości cosinusa.
Mamy już komplet informacji do obliczenia cosinusa, bowiem cosinus opisuje zależność między przyprostokątną leżącą przy kącie (u nas jest to \(|AO|=\frac{2\sqrt{3}}{3}\), a przeciwprostokątną (u nas jest to \(h_{b}=4\)). W związku z tym:
$$cosβ=\frac{\frac{2\sqrt{3}}{3}}{4} \\
cosβ=\frac{2\sqrt{3}}{3}\cdot\frac{1}{4} \\
cosβ=\frac{\sqrt{3}}{6}$$