Dany jest okrąg o środku S=(4,-3) i promieniu r=5. Liczba wszystkich punktów wspólnych tego okręgu z osiami

Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczmy podany środek i narysujmy okrąg o promieniu \(r=5\):


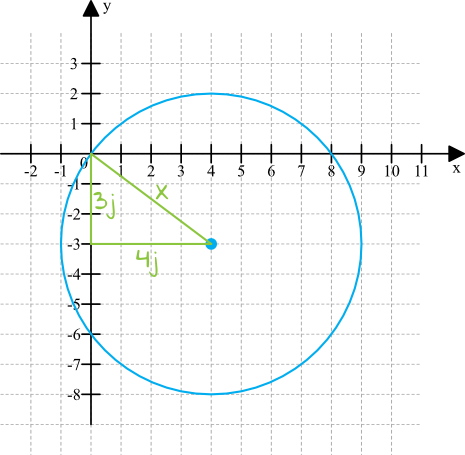
Krok 2. Obliczenie długości odcinka \(x\).
Z rysunku wynika, że nasz okrąg przecina początek układu współrzędnych i dlatego ma on trzy punkty wspólne z osiami układu współrzędnych. Nie mniej jednak dobrze byłoby się upewnić, czy rzeczywiście tak jest, bo rysunek szkicowy może nie być dokładny. Z tego też względu obliczmy długość odcinka \(x\), czyli odległość od początku układu współrzędnych do środka okręgu. Jeżeli ta długość będzie równa długości promienia (czyli będzie równa \(5\)), to nasz okrąg faktycznie będzie przechodził przez początek układu współrzędnych. Długość odcinka \(x\) obliczymy korzystając z Twierdzenia Pitagorasa:
$$3^2+4^2=x^2 \\
9+16=x^2 \\
x^2=25 \\
x=5 \quad\lor\quad x=-5$$

Ujemny wynik oczywiście odrzucamy, bo długość odcinka musi być dodatnia. Z tego też względu \(x=5\), czyli jest to dokładnie ta sama długość co nasz promień. To nas upewnia, że okrąg przechodzi przez środek układu współrzędnych i tym samym ma on \(3\) punkty wspólne z tym układem.