Rozwiązanie
Krok 1. Obliczenie długości boków podstawy.
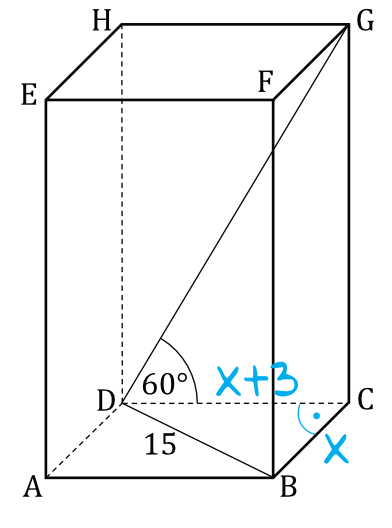
Spójrzmy na trójkąt \(BCD\), w którym znamy długość przeciwprostokątnej. Jeśli długość boku \(BC\) oznaczymy jako \(x\), to zgodnie z treścią zadania bok \(CD\) będzie mieć długość \(x+3\).
Korzystając zatem z Twierdzenia Pitagorasa, możemy zapisać, że:
$$x^2+(x+3)^2=15^2 \\
x^2+x^2+6x+9=225 \\
2x^2+6x=216 \\
2x^2+6x-216=0 \\
x^2+3x-108=0$$
Tak na marginesie, nie ma konieczności dzielenia całego równania przez \(2\) (tak jak ja to zrobiłem na samym końcu), ale dzięki temu później będziemy mieć mniejsze liczby.
Krok 2. Rozwiązanie powstałego równania kwadratowego.
W trakcie obliczeń otrzymaliśmy równanie kwadratowe w postaci ogólnej, więc rozwiążemy je przy pomocy delty:
Współczynniki: \(a=1,\;b=3,\;c=-108\)
$$Δ=b^2-4ac=3^2-4\cdot1\cdot(-108)=9-(-432)=441 \\
\sqrt{Δ}=\sqrt{441}=21$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-3-21}{2\cdot1}=\frac{-24}{2}=-12 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-3+21}{2\cdot1}=\frac{18}{2}=9$$
Krok 3. Obliczenie długości \(BC\) oraz \(CD\).
Wyszło nam, że rozwiązaniem równania jest \(x=-12\) oraz \(x=9\), ale oczywiście ujemny wynik musimy odrzucić, ponieważ długość boku musi być dodatnia. Stąd też zostaje nam \(x=9\), czyli tym samym (zgodnie z oznaczeniami) \(|BC|=9\) oraz \(|CD|=9+3=12\).
Krok 4. Obliczenie wysokości graniastosłupa.
Spójrzmy na trójkąt \(DCG\). Jest to trójkąt prostokątny, w którym znamy długość dolnej przyprostokątnej \(|CD|=9+3=12\) i znamy miarę kąta ostrego \(|\sphericalangle CDG|=60°\). Chcąc obliczyć wysokość graniastosłupa (czyli bok \(CG\)) możemy więc wykorzystać funkcje trygonometryczne, a konkretnie tangensa:
$$tg60°=\frac{H}{12} \\
\sqrt{3}=\frac{H}{12} \\
H=12\sqrt{3}$$
Krok 5. Obliczenie pola powierzchni bocznej.
Mamy już wszystkie miary krawędzi graniastosłupa. Pole powierzchni bocznej stanowią dwa prostokąty o wymiarach \(9\times12\sqrt{3}\) i dwa prostokąty o wymiarach \(12\times12\sqrt{3}\), zatem:
$$P_{b}=2\cdot9\cdot12\sqrt{3}+2\cdot12\cdot12\sqrt{3} \\
P_{b}=216\sqrt{3}+288\sqrt{3} \\
P_{b}=504\sqrt{3}$$
Krok 6. Obliczenie objętości graniastosłupa.
Celem zadania jest także obliczenie objętości, zatem:
$$V=9\cdot12\cdot12\sqrt{3} \\
V=1296\sqrt{3}$$