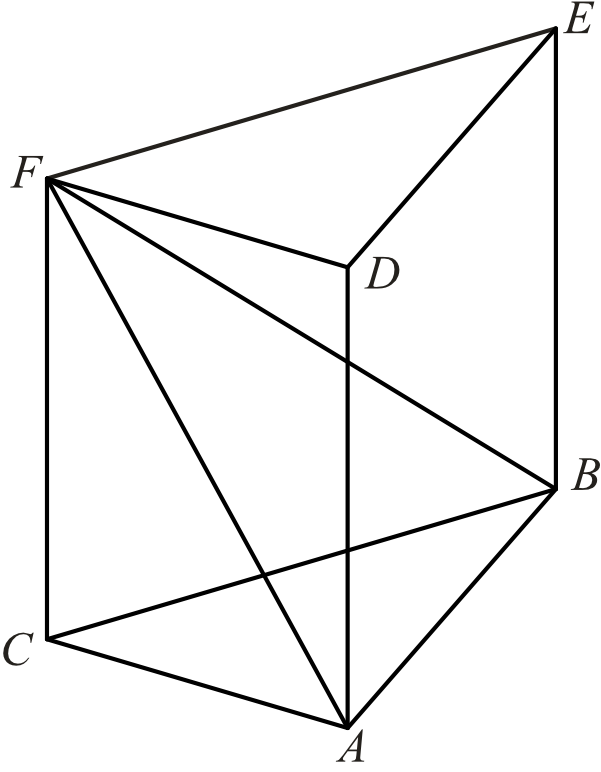
Dany jest graniastosłup prawidłowy trójkątny \(ABCDEF\) o podstawach \(ABC\) i \(DEF\) i krawędziach bocznych \(AD\), \(BE\) i \(CF\) (zobacz rysunek). Długość krawędzi podstawy \(AB\) jest równa \(8\), a pole trójkąta \(ABF\) jest równe \(52\). Oblicz objętość tego graniastosłupa.
Dorysujmy do głównego rysunku dwie wysokości – pierwszą niech będzie wysokość trójkąta \(ABC\) oraz drugą, tym razem trójkąta \(ABF\). Dodatkowo podpiszmy długości poszczególnych boków, a skoro jest to graniastosłup prawidłowy trójkątny, to w podstawie mamy trójkąt równoboczny, czyli więc wszystkie krawędzie podstawy mają długość \(8\).
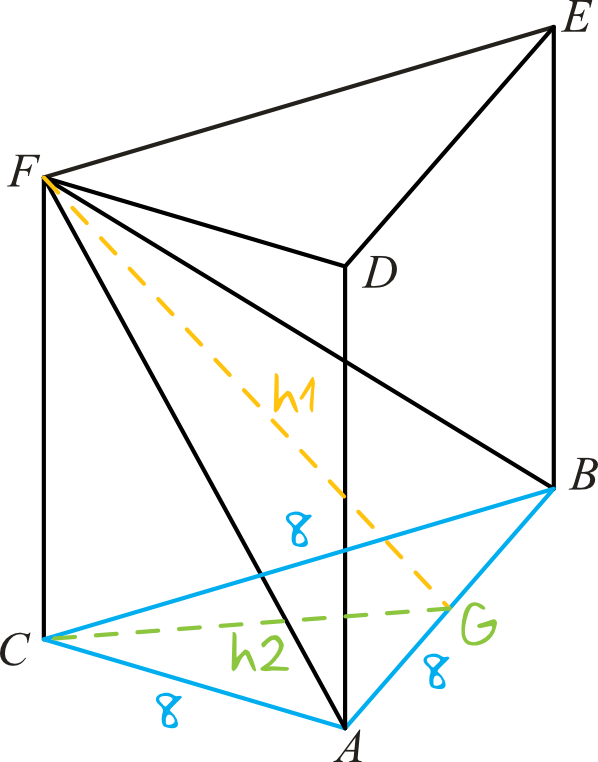
Możemy dostrzec, że trójkąt \(ABF\) jest trójkątem równoramiennym (obydwa ramiona są przekątnymi identycznych ścian bocznych). Korzystając więc z pola trójkąta podanego w treści zadania (\(P=52\)) oraz długości podstawy trójkąta (\(a=8\)) możemy obliczyć wysokość trójkąta \(ABF\):
$$P=\frac{1}{2}a\cdot h_{1} \\
52=\frac{1}{2}\cdot8\cdot h_{1} \\
52=4h_{1} \\
h_{1}=13$$
Wysokość \(|FG|\) jest więc równa \(13\).
Jak już sobie ustaliliśmy – w podstawie jest trójkąt równoboczny o boku długości \(a=8\). Jego wysokość możemy więc obliczyć korzystając z następującego wzoru:
$$h_{2}=\frac{a\sqrt{3}}{2} \\
h_{2}=\frac{8\sqrt{3}}{2} \\
h_{2}=4\sqrt{3}$$
Wysokość \(|CG|\) jest więc równa \(4\sqrt{3}\).
Do obliczenia objętości potrzebna nam jest oczywiście wysokość graniastosłupa. Wyznaczymy ją przy pomocy Twierdzenia Pitagorasa z trójkąta \(FCG\):
$$|FC|^2+|CG|^2=|FG|^2 \\
|FC|^2+(4\sqrt{3})^2=13^2 \\
|FC|^2+16\cdot3=169 \\
|FC|^2+48=169 \\
|FC|^2=121 \\
|FC|=11$$
Wysokość całego graniastosłupa jest więc równa \(H=11\).
Skoro w podstawie znajduje się trójkąt równoboczny, to jego pole jest równe:
$$P=\frac{a^2\sqrt{3}}{4} \\
P=\frac{8^2\sqrt{3}}{4} \\
P=\frac{64\sqrt{3}}{4} \\
P=16\sqrt{3}$$
Mamy już wszystkie dane, tak więc możemy przystąpić do obliczenia objętości:
$$V=P_{p}\cdot H \\
V=16\sqrt{3}\cdot11 \\
V=176\sqrt{3}$$
\(V=176\sqrt{3}\)

