Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania będzie wyglądać następująco:
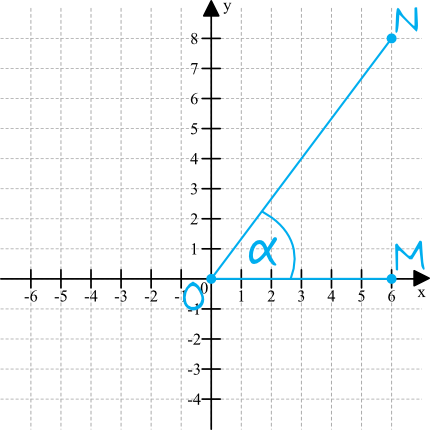
Krok 2. Obliczenie tangesa kąta \(MON\).
Z własności tangensów (możemy znaleźć je w tablicach maturalnych) wynika, że kiedy jedno ramię kąta pokrywa się z osią \(OX\), a wierzchołek jest w punkcie \((0,0)\) (a obydwie te rzeczy mają tutaj miejsce), to \(tg\alpha=\frac{y}{x}\), gdzie \(x\) oraz \(y\) to współrzędne dowolnego punktu, który leży na drugim ramieniu. My znamy współrzędne takiego punktu i jest nim \(N=(6,8)\), zatem podstawiając \(x=6\) oraz \(y=8\), otrzymamy:
$$tg\alpha=\frac{y}{x} \\
tg\alpha=\frac{8}{6} \\
tg\alpha=\frac{4}{3}$$