Rozwiązanie
Krok 1. Wyznaczenie współrzędnych wierzchołka paraboli.
Z treści zadania możemy odczytać bardzo ważną informację, a mianowicie współrzędne wierzchołka paraboli. Zastanówmy się co to znaczy, że funkcja rośnie w przedziale \((-\infty,2\rangle\) i że osiąga największą wartość równą \(10\). To by oznaczało, że nasza funkcja wygląda mniej więcej w ten sposób:
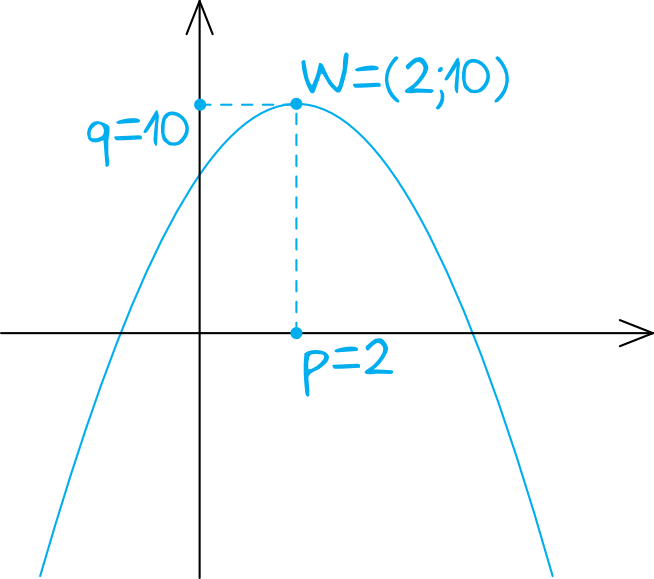
Wynika z tego, że funkcja ma wierzchołek w punkcie \(W=(2,10)\).
Krok 2. Zapisanie wzoru funkcji w postaci kanonicznej.
Znając współrzędne wierzchołka paraboli możemy zapisać ją w postaci kanonicznej:
$$f(x)=a(x-p)^2+q \\
f(x)=a(x-2)^2+10$$
Krok 3. Podstawienie współrzędnych punktu \(A\) oraz wyznaczenie współczynnika \(a\).
Do wyznaczonej przed chwilą postaci kanonicznej możemy podstawić współrzędne znanego nam punktu \(A\), co pozwoli wyznaczyć nam już jeden ze współczynników:
$$f(x)=a(x-2)^2+10 \\
-2=a(4-2)^2+10 \\
-2=a\cdot2^2+10 \\
-2=4a+10 \\
4a=-12 \\
a=-3$$
Krok 4. Wyznaczenie współczynników \(b\) oraz \(c\).
Znając współczynnik kierunkowy \(a=-3\) wiemy już, że w postaci kanonicznej nasza funkcja przyjmuje wzór:
$$f(x)=-3(x-2)^2+10$$
Jeżeli wykonamy teraz potęgowanie, to doprowadzimy funkcję do postaci ogólnej, co z kolei pozwoli nam odczytać wartości wszystkich współczynników:
$$f(x)=-3(x-2)^2+10 \\
f(x)=-3(x^2-4x+4)+10 \\
f(x)=-3x^2+12x-12+10 \\
f(x)=-3x^2+12x-2$$
To oznacza, że interesująca nas funkcja ma współczynniki:
$$a=-3,\;b=12,\;c=-2$$