Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować sobie tę sytuację. Wykresem funkcji będzie parabola (bo jest to funkcja kwadratowa), której ramiona są skierowane do góry (bo współczynnik kierunkowy \(a\) jest dodatni).
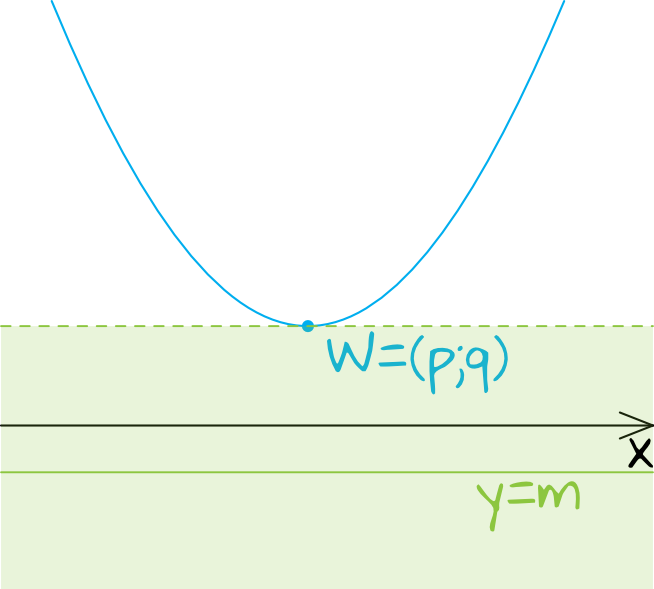
Prosta \(y=m\) jest prostą która przyjmuje jednakową wartość dla wszystkich argumentów (np. dla \(m=3\) mielibyśmy prostą \(y=3\)). Skoro prosta \(y=m\) ma nie mieć z naszą parabolą punktów wspólnych, to znaczy że musi znaleźć się pod parabolą (czyli w tej zielonej części na rysunku). Jaki z tego płynie wniosek? Wystarczy, że poznamy współrzędną igrekową wierzchołka naszej paraboli i będziemy wiedzieć od jakiej wartości musi być mniejszy nasz parametr \(m\).
Krok 2. Obliczenie współrzędnej \(q\) wierzchołka paraboli.
Szukamy współrzędnej \(q\) wierzchołka (czyli współrzędnej igrekowej). Możemy to zrobić za pomocą wzoru:
$$q=-\frac{Δ}{4a}=-\frac{b^2-4ac}{4a}$$
Współczynniki: \(a=1,\;b=4,\;c=10\)
$$q=-\frac{4^2-4\cdot1\cdot10}{4\cdot1} \\
q=-\frac{16-40}{4} \\
q=-\frac{-24}{4} \\
q=-(-6) \\
q=6$$
Krok 3. Ustalenie zbioru do którego należy liczba \(m\).
Nasza liczba \(m\) musi być mniejsza od \(6\) (bo dla \(m=6\) prosta \(y=m\) przecięłaby parabolę dokładnie w wierzchołku), zatem interesuje nas zbiór \((-\infty,6)\).