Rozwiązanie
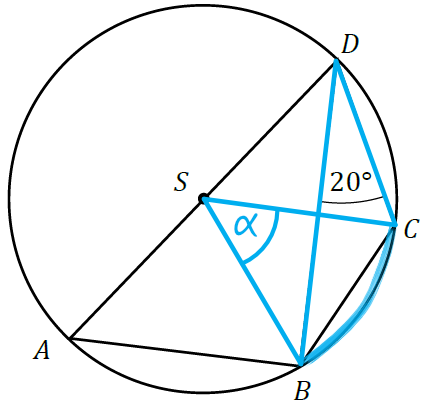
Kąt \(BSC\) jest kątem środkowym, który jest oparty na tym samym łuku, co kąt \(BDC\) o mierze \(20°\). Z własności kątów środkowych i wpisanych wiemy, że w takiej sytuacji miara kąta środkowego musi być dwa razy większa, zatem:
$$|\sphericalangle BSC|=2\cdot20° \\
|\sphericalangle BSC|=40°$$