Rozwiązanie
Aby dowiedzieć się ile wyrazów ujemnych ma wskazany ciąg musimy rozwiązać następującą nierówność:
$$4(n+1)(n-10)\lt0 \quad\bigg/:4 \\
(n+1)(n-10)\lt0$$
Krok 2. Rozwiązanie powstałej nierówności kwadratowej.
Otrzymaliśmy nierówność kwadratową zapisaną w postaci iloczynowej. Rozwiązywanie nierówności rozpoczynamy od wyznaczenia miejsc zerowych, czyli sprawdzenia kiedy \((n+1)(n-10)=0\). Zgodnie z własnościami postaci iloczynowej możemy zapisać, że:
$$n+1=0 \quad\lor\quad n-10=0 \\
n=-1 \quad\lor\quad n=10$$
Zaznaczamy na osi nasze wyznaczone miejsca zerowe (kropki będą niezamalowane, bo w nierówności mamy znak \(\lt\)) i szkicujemy parabolę. Parabola będzie mieć ramiona skierowane do góry, bo współczynnik kierunkowy \(a\) jest dodatni, zatem:
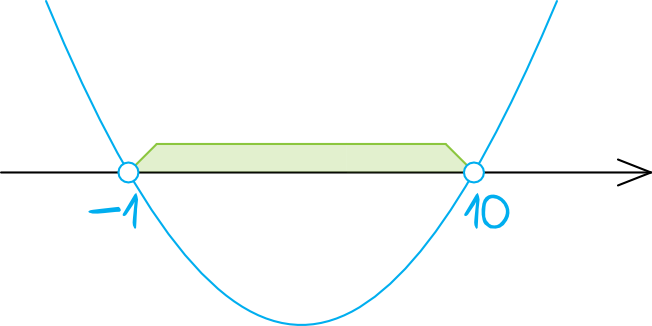
Teraz musimy odczytać rozwiązania naszej nierówności. Interesują nas wartości mniejsze od zera, czyli wszystko to, co znalazło się pod osią. Możemy więc zapisać, że rozwiązaniem tej nierówności jest przedział \(n\in(-1;10)\).
Krok 3. Interpretacja otrzymanego wyniku.
Ze wszystkich dotychczasowych obliczeń wyszło nam, że \(4(n+1)(n-10)\) jest mniejsze od zera dla każdego \(n\), które jest większe od \(-1\) i mniejsze od \(10\). W przypadku ciągów \(n\) musi być dodatnią liczbą naturalną. Musimy więc sprawdzić jakie liczby naturalne mieszczą się w wyznaczonym przez nas przedziale. Takimi liczbami będą: \(1,2,3,4,5,6,7,8,9\). Pasuje nam \(9\) liczb, zatem ten ciąg ma \(9\) wyrazów ujemnych.