Rozwiązanie
Krok 1. Ułożenie nierówności kwadratowej.
Chcąc sprawdzić ile jest dodatnich wyrazów naszego ciągu musimy sprawdzić kiedy \((5-n)\cdot(n+3)\) jest większe od zera. To oznacza, że musimy rozwiązać następującą nierówność:
$$(5-n)\cdot(n+3)\gt0$$
Krok 2. Rozwiązanie nierówności kwadratowej.
Powstała nam klasyczna nierówność kwadratowa, którą musimy teraz rozwiązać. Pierwszym krokiem ku temu jest tradycyjnie wyznaczenie miejsc zerowych, czyli sprawdzenie kiedy \((5-n)\cdot(n+3)\) jest równe \(0\). Oczywiście możemy wymnożyć przez siebie poszczególne nawiasy, otrzymując w ten sposób postać ogólną z której potem wyliczymy deltę, ale istnieje szybszy sposób na rozwiązanie tego przykładu. Aby \((5-n)\cdot(n+3)\) było równe \(0\), to albo wartość w tym pierwszym nawiasie jest równa \(0\), albo w tym drugim (dokładnie tak jak w postaci iloczynowej). Z tego też względu:
$$5-n=0 \quad\lor\quad n+3=0 \\
n=5 \quad\lor\quad n=-3$$
Teraz zaznaczamy te dwa miejsca zerowe na naszej osi liczbowej (kropki będą niezamalowane, bo w nierówności mamy znak \(\gt\)) i przystępujemy do rysowania paraboli. Musimy jeszcze tylko ustalić, czy ramiona paraboli będą skierowane do góry, czy do dołu. No i tu jest spora pułapka, bo ramiona paraboli będą skierowane do dołu, co najlepiej będzie widać, gdy wymnożymy przez siebie te dwa nawiasy:
$$(5-n)\cdot(n+3)=5n+15-n^2-3n=-n^2+2n+15$$
Przed \(n^2\) mamy minusa, czyli współczynnik kierunkowy \(a\) jest ujemny. Stąd też ramiona paraboli muszą być skierowane do dołu. Nasz wykres będzie więc wyglądał w ten oto sposób:
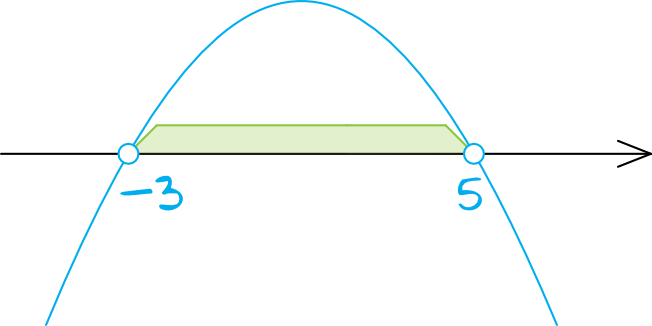
Z wykresu wynika, że rozwiązaniem naszej nierówności kwadratowej jest przedział \(n\in(-3;5)\).
Krok 3. Interpretacja otrzymanego wyniku.
To jednak nie jest koniec zadania. Z własności ciągów wiemy, że \(n\) musi być liczbą naturalną, bo nie ma czegoś takiego jak np. "półtorazowy wyraz". To oznacza, że z przedziału \(n\in(-3;5)\) musimy jeszcze wyodrębnić liczby naturalne. W tym przedziale znajdą się cztery takie liczby: \(1,2,3,4\) (piątka jest poza przedziałem, bo nawias nie jest domknięty), co matematycznie możemy zapisać jako \(n\in\{1,2,3,4\}\). To oznacza, że tylko cztery wyrazy tego ciągu są liczbami dodatnimi - pierwszy, drugi, trzeci oraz czwarty.