Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Bryły obrotowe. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Prostokąt o wymiarach \(5\times7\) zaczęto obracać wokół krótszego boku. Objętość powstałego walca jest równa:
Zadanie 2. (1pkt) Promień podstawy stożka ma długość \(r=6\), a pole przekroju osiowego wynosi \(P=24\). Objętość tego stożka jest równa:
Zadanie 3. (1pkt) 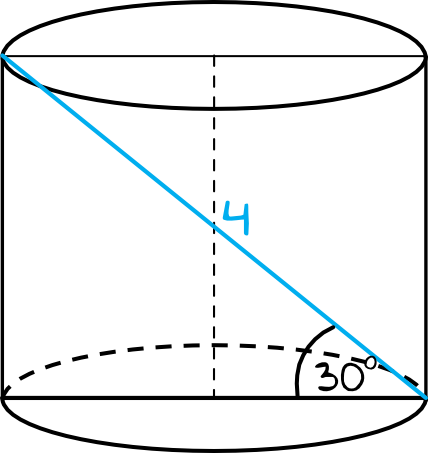
Objętość powyższego walca jest równa:
Zadanie 4. (1pkt) Kąt nachylenia tworzącej stożka do podstawy jest równy \(45°\). Tworząca stożka ma długość \(3\sqrt{2}\). Objętość stożka wynosi:
Zadanie 5. (1pkt) Trójkąt równoboczny o polu \(P=9\sqrt{3}\) zaczęto obracać wzdłuż jego osi symetrii. Pole powierzchni całkowitej tego stożka jest równe:
Zadanie 6. (1pkt) W przekroju osiowym stożka prawidłowego znajduje się zawsze trójkąt równoramienny lub równoboczny, a podstawa tego trójkąta ma długość \(2r\).
Zadanie 7. (1pkt) Tworząca stożka jest dwukrotnie dłuższa od wysokości bryły. W takiej sytuacji kąt rozwarcia stożka ma miarę \(60°\).
Zadanie 8. (1pkt) Pewna pralinka w kształcie kuli o promieniu \(r=1cm\) ma zewnętrzną warstwę czekolady o grubości \(0,3cm\). Cała wewnętrzna część praliny wypełniona jest nadzieniem. Jaś twierdzi, że objętość nadzienia jest większa niż objętość czekolady. Małgosia uważa, że jednak objętościowo mamy więcej czekolady niż nadzienia. Kto ma rację?
Zadanie 9. (1pkt) Kartkę A4 o wymiarach \(29,7cm\times21cm\) zwinięto w rulon w taki sposób, że złączono ze sobą dwa krótsze brzegi kartki, tworząc w ten sposób powierzchnię boczną walca. Jaka jest objętość tego walca? Do obliczeń przyjmij przybliżenie \(π\approx3,14\).
Zadanie 10. (1pkt) Dany jest walec o wysokości \(6\). Jaka jest objętość tego walca, jeżeli jego pole powierzchni bocznej stanowi \(\frac{1}{3}\) pola powierzchni całkowitej?
