Rozwiązanie
Krok 1. Ustalenie, która prosta jest prostą \(AC\), a która \(BC\).
Skąd wiemy, która prosta jest opisana równaniem \(y=\frac{2}{3}x+2\), a która \(y=-x+2\)? By to stwierdzić, nie musimy tutaj wykonywać żadnych większych obliczeń. Wystarczy zauważyć, że jedna prosta jest rosnąca (czyli jej współczynnik kierunkowy \(a\) musi być dodatni), a druga jest malejąca (czyli jej współczynnik \(a\) musi być ujemny). To prowadzi nas do wniosku, że prosta \(AC\) wyraża się równaniem \(y=\frac{2}{3}x+2\), natomiast prosta \(BC\) wyraża się równaniem \(y=-x+2\).
Krok 2. Wyznaczenie współrzędnych punktów \(A\), \(B\) oraz \(C\).
Zacznijmy od punktu \(A\). Widzimy, że leży on na osi \(Ox\), czyli jego współrzędna \(y=0\). Skoro punkt \(A\) leży na prostej \(y=\frac{2}{3}x+2\), to podstawiając do tego równania \(y=0\), otrzymamy:
$$0=\frac{2}{3}x+2 \\
-2=\frac{2}{3}x \\
x=-3$$
To oznacza, że \(A=(-3;0)\).
Analogicznie podchodzimy do punktu \(B\), bo tutaj także \(y=0\), ale tym razem równaniem prostej przechodzącej przez ten punkt będzie \(y=-x+2\), tak więc:
$$0=-x+2 \\
x=2$$
To oznacza, że \(B=(2;0)\).
Wyznaczenie współrzędnych punktu \(C\) jest najprostsze, ponieważ jest to punkt leżący na osi \(Oy\), a więc z pomocą przyjdzie nam współczynnik \(b\) prostej, która przez ten punkt przechodzi. Widzimy wyraźnie, że zarówno jedna, jak i druga prosta, mają współczynnik \(b=2\), tak więc \(C=(0;2)\).
Krok 3. Obliczenie pola powierzchni trójkąta \(ABC\).
Nanosząc na rysunek obliczone współrzędne, otrzymamy taką oto sytuację:
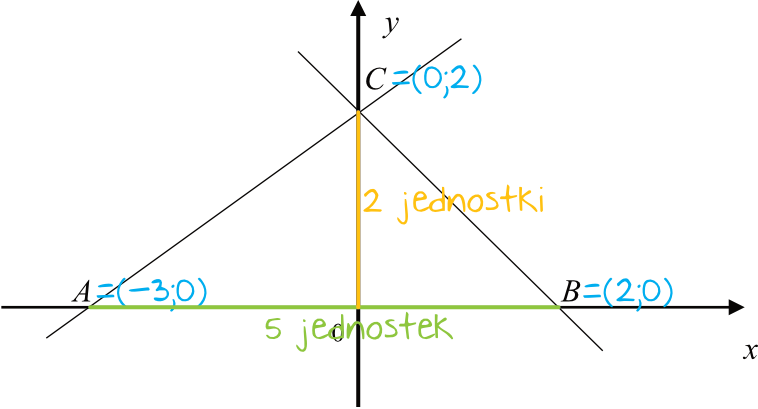
Licząc nawet po kratkach widzimy, że podstawa naszego trójkąta ma długość \(a=5\), natomiast wysokość tego trójkąta to \(h=2\). Skoro tak, to korzystając ze standardowego wzoru na pole trójkąta, możemy zapisać, że:
$$P=\frac{1}{2}ah \\
P=\frac{1}{2}\cdot5\cdot2 \\
P=5$$