Pewnie nieraz widziałeś w książce lub podręczniku narysowane kontury Polski. Na pewno miałeś też styczność z różnymi mapami, zarówno tymi elektronicznymi jak i papierowymi. Charakterystycznym elementem tych wszystkich grafik jest to, że przedstawiają one rzeczywistość w pewnym pomniejszeniu, tak by cały obraz mógł zmieścić się czy to na kartce papieru, czy ekranie komputera. Wszystkie te odzwierciedlenia możliwe są dzięki zastosowaniu skali, która określa nam jak bardzo dany przedmiot został pomniejszony lub powiększony.
Czym jest skala i jaką ją odczytać?
Jeżeli mamy przedmiot w skali \(1:1\) to znaczy, że wymiary przedmiotu na kartce są dokładnie takie same jak w rzeczywistości. Jeśli więc przyłożysz telefon do zeszytu i odrysujesz go, to będzie on narysowany dokładnie w skali \(1:1\).
Skala \(2:1\) oznacza, że narysowany przedmiot ma wymiary dwa razy większe od pierwowzoru. Jeśli więc twój telefon ma długość \(14cm\) i szerokość \(6cm\), to narysowany w skali \(2:1\) będzie miał długość \(28cm\) (bo \(14cm\cdot2=28cm\)) i szerokość \(12cm\) (bo \(6cm\cdot2=12cm\)).
Skala \(1:2\) oznacza, że narysowany przedmiot ma wymiary dwa razy mniejsze od pierwowzoru. Jeśli więc chcielibyśmy ten sam telefon o wymiarach \(14cm\) i \(6cm\) narysować w skali \(1:2\) to otrzymalibyśmy rysunek o wysokości \(7cm\) (bo \(14cm:2=7cm\)) i szerokości \(3cm\) (bo \(6cm:2=3cm\)).
Zadanie jest bardzo proste do obliczenia, bo wystarczy wykonać jedno proste mnożenie (dokładnie takie jak robiliśmy powyżej). Długość samochodu jest równa:
$$20cm\cdot24=480cm$$
Rodzaje skal:
Możemy spotkać się z następującymi rodzajami skal:
- liczbowa – to tradycyjna skala, którą wyrażamy w formie liczb, np. \(1:10\;000\) lub \(1:500\;000\)
- mianowana – bardzo podobna do liniowej, z tą jednak różnicą, że już jest przeliczona na jednostki np. \(1cm – 5km\) lub \(1cm – 200m\)
- liniowa – ta skala zawiera podziałkę, która wizualnie pokazuje ile metrów/kilometrów w rzeczywistości odpowiada odległości narysowanego odcinka
Zadania kontrolne:
- Odpowiedź: Na podstawie informacji zawartej w skali wiemy, że \(1cm\) na mapie odpowiada \(2000cm\) w rzeczywistości. Dobrze jest od razu sobie centymetry zamienić na np. metry, a skoro \(100cm=1m\), to \(2000cm=20m\).
Teraz musimy zrobić bardzo prostą i logiczną proporcję. Skoro \(1cm\) na mapie odpowiada odległości \(20m\), to ile metrów w rzeczywistości ma odcinek \(4cm\)? Oczywiście ta odległość będzie cztery razy większa, tak więc:
$$20m\cdot4=80m$$
Rzeczywista odległość między tymi punktami wynosi więc \(80\) metrów.
- Odpowiedź: Ze skali odczytujemy informację, że \(1cm\) na mapie jest równy \(100cm\) w rzeczywistości, czyli że \(1cm\) na mapie jest tak naprawdę równy odległości \(1m\) (bo \(100cm=1m\)). Skoro \(1cm\) jest równy \(1m\), to ile centymetrów na mapie musi mieć ten odcinek aby był on równowartością \(12m\)? Oczywiście będzie on odpowiednio dwanaście razy dłuższy, czyli będzie miał \(12cm\).
Zadanie możemy też wykonać innym sposobem, zamieniając wszystkie jednostki na centymetry, spójrz:
Dystans pomiędzy punktami to \(12m\), czyli \(1200cm\). Na mapie ta odległość wyniesie więc:
$$1200cm:100=12cm$$
(Dzielimy przez \(100\), bo skala jest \(1:100\). Gdyby skala wynosiła np. \(1:60\) to dzielilibyśmy przez \(60\)).Przy tego typu zadaniach zachęcam Cię do korzystania zarówno z jednego i drugiego sposobu, w zależności od tego którym wygodniej Ci się rozwiązuje zadania.
Ćwiczenia powiązane z tym tematem:

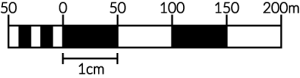
super
fajne
super
Ta strona pomaga mi się uczyć do sprawdzianów.
bardzo fajna stronka oprócz nauki do spr można też rozwiązywać quizy. polecam
Strona bardzo pomocna i łatwo pomaga rozwiązać zadania których się nie rozumie.
Świetne
Jestem kompletnym mongołkiem jeśli chodzi o matematykę. Chciałem powiedzieć że z pomocą tego tutaj właśnie tekstu mając 22 lata zrozumiałem jak obliczać skalę. Pozdrawiam!
Jutro pisze z tego sprawdzian tylko że poprawę
fajna stronka lubie sobie na niej uczyć
fajne i pożyteczne
super stronka.Polecam
Super przydatne
spk ;)
Przydało mi się do matmy bo miałem pracę domową o treści „Wyszukaj w internecie zadania z planem i mapa”
te sprawdziany i tematy są bardzo fajne można się poduczyć różnych ciekawych tematów a potem mieć same 5 i 6 (tak jak ja)
strona naprawdę jest fajna. Dostałam 1 ze sprawdzianu a poprawiłam na 4- :] POZDRAWIAM
Super jest ta stronka pomaga mi się uczyć do testów
a ja sądzę, że z tej strony można wyciągnąć same przydatne rzeczy.
Pozdrawiam Sąsiad z ulicy Sezamkowej! ;)
spoko zadania