W czwartej klasie nauczymy się obliczać pole prostokąta i kwadratu. W kolejnych klasach poznasz też wzory na wyliczenie pola trójkąta, rombu, równoległoboku czy też trapezu. Obliczenie pola prostokąta i kwadratu jest tak naprawdę bardzo proste, bo sprowadza się do pomnożenia przez siebie dwóch liczb. Spójrzmy na przykład:
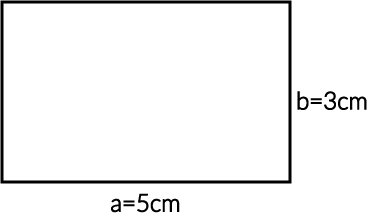
Aby móc obliczyć pole powierzchni wystarczy pomnożyć jego długość i szerokość. W naszym przypadku wystarczy więc pomnożyć przez siebie \(5cm\) i \(3cm\), co da nam wynik:
$$P=5cm\cdot3cm=15cm^2$$
Identycznie obliczymy pole kwadratu, choć tu wystarczy znać długość jednego boku (wszak wszystkie boki w kwadracie są równej długości). Jeśli więc chcemy obliczyć pole kwadratu o boku \(4cm\), to wystarczy wykonać działanie:
$$P=4cm\cdot4cm=16cm^2$$
Jak więc widzisz obliczenia te nie są trudne, ale trzeba uważać na jedną rzecz – jednostki. W naszym przykładzie wymiary boków były wyrażone w tych samych jednostkach (centymetrach). Jeżeli w jakimś zadaniu będziesz mieć dwie różne jednostki (np. prostokąt o bokach \(5dm\) i \(3cm\)), to musisz koniecznie zamienić na takie, by wszystkie boki były wyrażone w jednej jednostce. Chcąc więc policzyć pole prostokąta o bokach \(5dm\) i \(3cm\) musimy zamienić \(5dm\) na \(50cm\) i wykonać działanie:
$$P=50cm\cdot3cm=150cm^2$$
Zamiana jednostek jest konieczna i logiczna, bo chyba nie masz wątpliwości że pole prostokąta o bokach \(5dm\) i \(3cm\) jest znacznie większe od tego o bokach \(5cm\) i \(3cm\).
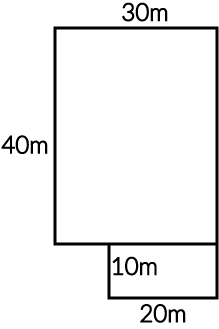
Musimy obliczyć pole powierzchni powyższej działki? Jak się do tego zabrać?
Na takie regularne kształty niestety nie ma wzorów matematycznych, musimy więc wykazać się sprytem i podzielić ten teren na dwa mniejsze prostokąty, o tak:
Teraz naszym zadaniem jest obliczenie powierzchni dwóch prostokątów i dodanie tych wartości do siebie. Pierwszy prostokąt ma wymiary \(30m\;x\;40m\), więc jego pole powierzchni jest równe:
$$P_{1}=30m\cdot40m=1200m^2$$
Drugi prostokąt ma wymiary \(20m\;x\;10m\), więc jego powierzchnia jest równa:
$$P_{2}=20m\cdot10m=200m^2$$
Łączna powierzchnia to w takim razie:
$$P=P_{1}+P_{2}=1200m^2+200m^2=1400m^2$$
Jeżeli więc zobaczysz nieregularną figurę w jakimś zadaniu, to spróbuj ją podzielić na mniejsze części, tak aby obliczyć cząstkowe pola powierzchni.
W zadaniach z polami powierzchni mogą przydać Ci się następujące tematy i ćwiczenia:


banał
Super strona, uczę wnuczka w oparciu o zamieszczone tutaj zadania.
Fajnie sporo się nauczyłem a co będzie jak będą dwie różne jednostki
W tym zadaniu tak się nie zdarzy, ale tak ogólnie to musimy zawsze ujednolicać jednostki – czyli sprowadzić wszystkie długości np. do centymetrów, metrów lub jakiejkolwiek innej jednostki długości :)
fajna strona, a jest gdzieś coś o polu trójkąta?
Pewnie, cała masa rzeczy na ten temat jest :)
Do poczytania: https://szaloneliczby.pl/pole-trojkata/
Do poćwiczenia: https://szaloneliczby.pl/oblicz-pole-trojkata/
Sprawdzian: https://szaloneliczby.pl/pole-trojkata-sprawdzian-klasa-6/
super strona bardzo dużo się nauczyłam :) polecę ją koleżankom :)
musiałam się tego nauczyć na kartkówkę jak mnie na lekcjach nie było i mi to bardzo pomogło dzięki
świetne to jest można się dużo nauczyć! A czy jest tu coś o procentach?
Przecież tutaj jest pełno rzeczy o procentach ;) Zajrzyj np. do klasy 6:
https://szaloneliczby.pl/klasa-6/
Dobre wytłumaczenie, ale akurat w tym zadaniu P1+P2 nie jest równe 1200 tylko 1400.
Pozdro.
P1 jest równe 1200, natomiast P2 jest równe 200. To oznacza, że P1+P2 jest równe 1200+200 czyli 1400 :)
banalne
dzięki jest proste do zrozumienia