Co to jest pole powierzchni?
Z pewnością nie raz słyszałeś o takich wielkościach jak metry kwadratowe, hektary lub kilometry kwadratowe. W tych pierwszych mierzymy np. wielkość mieszkania, w tych drugich wielkość działek, a w tych trzecich powierzchnię kraju. Pole powierzchni jest więc pewną miarą, którą opisujemy wielkość/rozmiar jakiegoś zamkniętego obszaru lub figury.
Jak zmierzyć pole powierzchni?
W przypadku mierzenia odległości sprawa była prosta – braliśmy linijkę lub centymetr i mierzyliśmy długość. A jak mierzymy pole powierzchni? Pól powierzchni tak naprawdę nie mierzymy, tylko je obliczamy. Nawet specjalistyczne narzędzia budowlane, które podają nam jakąś powierzchnię nie mierzą jej faktycznie, tylko wyliczają. Aby móc obliczyć takie pole powierzchni potrzebujemy po pierwsze pewnych długości, które musimy znać (lub wyznaczyć), a po drugie wzorów, do których podstawiamy zebrane dane. W kolejnych tematach będziemy właśnie poznawać różne sposoby oraz przede wszystkim wzory na obliczanie takich pól.
Brzmi to może dość skomplikowanie, ale to tylko pozory. W gruncie rzeczy prawie wszystko sprowadza się do wykonywania poprawnie prostych działań matematycznych (głównie mnożenia). Zanim jednak będziesz poznawać wszystkie sposoby na wyliczenie pola powierzchni zobaczmy jak zapisać i zinterpretować poszczególne jednostki.
\(1m^2\) to jednostka powierzchni, która jest równa polu kwadratu o boku \(1m\).
Analogicznie powierzchnię \(1cm^2\) będzie miał kwadrat o boku \(1cm\), a \(1km^2\) o boku \(1km\).
Bardzo częstym błędem w tym dziale jest stwierdzenie, że skoro kwadrat o boku \(1cm\) ma powierzchnię równą \(1cm^2\) to kwadrat o boku \(5cm\) ma pole równe \(5cm^2\). To ogromny błąd!
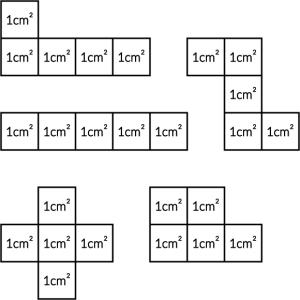
Pole powierzchni równe \(5cm^2\) otrzymamy np. wtedy, gdy połączymy ze sobą pięć kwadratów polu \(1cm^2\) i to niezależnie od sposobu ich ułożenia, spójrz:
Na powyższym przykładzie każda figura ma różny obwód, ma różną wysokość, ma różną szerokość, ale za każdym razem ma tą samą powierzchnię równą \(5cm^2\). I my tę własność będziemy bardzo często wykorzystywać przy rozwiązywaniu różnych zadań geometrycznych, gdzie będziemy dzielić jakieś figury na mniejsze części.
Więcej informacji na temat jednostek powierzchni oraz pól poszczególnych figur znajdziesz tutaj:

Ta strona jest super!!
właśnie to przerabiam i jest fajne do sprawdzenia się i do poćwiczenia
bardzo fajne jeśli ktoś tego nie rozumie albo się uczy. BARDZO POLECAM!!
Ja też. SUPER!!
Gorąco polecam tę stronę można się wiele nauczyć!!!